题目内容
sin10°+2sin10°sin20°sin40°= .
考点:三角函数中的恒等变换应用
专题:三角函数的求值
分析:利用积化和差公式对原式进行两次化简求得答案.
解答:
解:原式=sin10°+2sin10°•[
-
-]
=sin10°+sin10°•(cos20°-cos60°)
=sin10°-
sin10°+sin10°cos20°
=
sin10°+sin10°cos20°
=
[sin(10°-20°)+sin(10°+20°)]+
sin10°
=-
sin10°+
+
sin10°
=
,
故答案为:
| cos(20°-40°) |
| 2 |
| cos(20°+40°) |
| 2 |
=sin10°+sin10°•(cos20°-cos60°)
=sin10°-
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
=
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题主要考查了三角函数的恒等变换.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
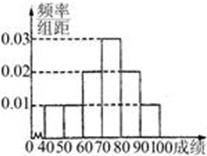 我校举办安全法规知识竞赛,从参赛的高一、高二学生中各抽出100人的成绩作为样本.对高一年级的100名学生的成绩进行统计,并按[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分组,得到成绩分布的频率分布直方图(如图).
我校举办安全法规知识竞赛,从参赛的高一、高二学生中各抽出100人的成绩作为样本.对高一年级的100名学生的成绩进行统计,并按[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分组,得到成绩分布的频率分布直方图(如图).