Question

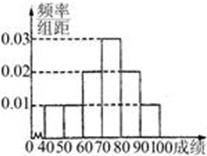我校举办安全法规知识竞赛，从参赛的高一、高二学生中各抽出100人的成绩作为样本．对高一年级的100名学生的成绩进行统计，并按[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]分组，得到成绩分布的频率分布直方图（如图）．
（Ⅰ）若规定60分以上为合格，计算高一年级这次知识竞赛的合格率；
（Ⅱ）若高二年级这次知识竞赛的合格率为60%，由以上统计数据填写下 面2×2列联表，并判断能否在犯错的概率不超过0.01的前提下认为“这次知识竞赛的成绩与年级有关系”．（K²小数点后保留一位小数）

合格情况 年级	合格人数	不合格人数	总计
高一
高二
总计

Answer 1

考点：独立性检验的应用

专题：应用题,概率与统计

分析：（Ⅰ）利用直方图，根据频率等于纵轴×组距，即可得到结论；
（Ⅱ）根据提供数据，可填写表格，利用公式，可计算K²的值，根据临界值表，即可得到结论．

解答： 解：（Ⅰ）由题意，高一年级这次知识竞赛的合格率为0.02×10+0.03×10+0.02×10+0.01×10=0.8=80%；
（Ⅱ）列联表如下

	高一	高二	合计
合格人数	80	60	140
不合格人数	20	40	60
合计	100	100	200

∴K²=

200(80×40-20×60)2

100×100×140×60

≈9.6＞6.635，
∴在犯错的概率不超过0.01的前提下认为“这次知识竞赛的成绩与年级有关系”．

点评：本题考查统计知识，考查学生的读图能力，考查学生的计算能力，属于中档题．