题目内容
集合A={x|(x-1)(2x-3)≤1},B={x|-1<x<
},则A∩B为( )
| 3 |
| 2 |
A、{x|
| ||||
B、{x|1<x≤
| ||||
C、{x|
| ||||
D、{x|
|
考点:交集及其运算
专题:集合
分析:求出A中不等式的解集确定出A,找出A与B的交集即可.
解答:
解:由A中的不等式变形得:2x2-5x+2≤0,即(2x-1)(x-2)≤0,
解得:
≤x≤2,即A={
≤x≤2};
∵B={x|-1<x<
},
∴A∩B={x|
<x<
}.
故选:D.
解得:
| 1 |
| 2 |
| 1 |
| 2 |
∵B={x|-1<x<
| 3 |
| 2 |
∴A∩B={x|
| 1 |
| 2 |
| 3 |
| 2 |
故选:D.
点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
下列判断错误的是( )
| A、命题“?x∈R,2x>0”的否定是“?x0∈R,2x0≤0” | ||||
| B、命题“若xy=0,则x=0”的否命题为“若xy≠0,则x≠0” | ||||
| C、函数y=2x-3+1的图象恒过定点A(3,2) | ||||
D、“sinα=
|
已知x,y满足约束条件
,则z=x+
y的最小值为( )
|
| 1 |
| 2 |
A、
| ||
B、
| ||
| C、1 | ||
| D、3 |
下列命题中的真命题是( )
| A、若a>b>0,a>c,则a2>bc | ||||
B、若a>b>c,则
| ||||
| C、若a>b,n∈N*,则an>bn | ||||
| D、若a>b>0,则1na<1nb |
下列说法正确的是( )
| A、“a>b”是“a2>b2”的必要条件 |
| B、自然数的平方大于0 |
| C、“若a,b都是偶数,则a+b是偶数”的否命题为真 |
| D、存在一个钝角三角形,它的三边长均为整数 |
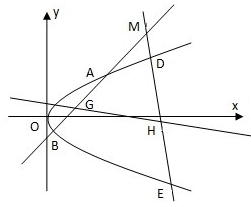 已知抛物线C:y2=2px(p>0),M点的坐标为(12,8),N点在抛物线C上,且满足
已知抛物线C:y2=2px(p>0),M点的坐标为(12,8),N点在抛物线C上,且满足