题目内容
把甲、乙、丙、丁、戊5人分配去参加三项不同的活动,其中活动一和活动二各要2人,活动三要1人,且甲,乙两人不能参加同一活动,则一共有 种不同分配方法.
考点:组合及组合数公式
专题:排列组合
分析:间接法:先求出活动一和活动二各要2人,活动共有三要1人的方法种数,去掉甲,乙两人参加同一活的方法种数即可.
解答:
解:由题意把甲、乙、丙、丁、戊5人分配去参加三项不同的活动,
其中活动一和活动二各要2人,活动三要1人共有
=30种方法,
其中甲,乙两人参加同一活动
+
=6种方法,
故符合题意得方法共30-6=24种,
故答案为:24.
其中活动一和活动二各要2人,活动三要1人共有
| C | 2 5 |
| C | 2 3 |
其中甲,乙两人参加同一活动
| C | 2 3 |
| C | 2 3 |
故符合题意得方法共30-6=24种,
故答案为:24.
点评:本题考查排列组合的应用,间接法是解决问题的关键,属基础题.

练习册系列答案
相关题目
已知i是虚数单位,则
=( )
| 3-i |
| 1+i |
| A、2+i | B、2-i |
| C、1+2i | D、1-2i |
集合A={x|(x-1)(2x-3)≤1},B={x|-1<x<
},则A∩B为( )
| 3 |
| 2 |
A、{x|
| ||||
B、{x|1<x≤
| ||||
C、{x|
| ||||
D、{x|
|
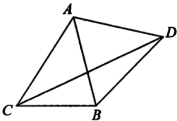 如图,△ABC中.角A、B、C所对边的长分别为a、b、c满足c=l,a2+b2=ab+1,以AB为边向△ABC外作等边三角形△ABD.
如图,△ABC中.角A、B、C所对边的长分别为a、b、c满足c=l,a2+b2=ab+1,以AB为边向△ABC外作等边三角形△ABD.