题目内容
已知函数f(x)=x2-mx+m-1.
(1)若函数y=lgf(x)在[2,4]上有意义,求实数m的取值范围;
(2)若函数y=|f(x)|在[-1,0]上单调递减,求实数m的取值范围;
(3)若对于区间[2,
]内任意两个相异实数x1,x2,总有|f(x1)-f(x2)|≤|x1-x2|成立,求实数m的取值范围.
(1)若函数y=lgf(x)在[2,4]上有意义,求实数m的取值范围;
(2)若函数y=|f(x)|在[-1,0]上单调递减,求实数m的取值范围;
(3)若对于区间[2,
| 5 |
| 2 |
考点:二次函数的性质,函数的值域
专题:函数的性质及应用
分析:(1)若函数y=lgf(x)在[2,4]上有意义,则x2-mx+m-1>0,对任意的x∈[2,4]恒成立,即m(x-1)<x2-1对任意的x∈[2,4]恒成立,即m<x+1对任意的x∈[2,4]恒成立,进而可得实数m的取值范围;
(2)结合函数y=|f(x)|的图象和性质,由[-1,0]上单调递减,分类讨论满足条件的实数m的取值范围,最后综合讨论结果,可得答案;
(3)若对于区间[2,
]内任意两个相异实数x1,x2,且f(x1)-f(x2)=(x1-x2)(x1+x2-m)|(x1-x2)(x1+x2-m)|≤|x1-x2|(x1≠x2)恒成立,|m-(x1+x2)|≤1对任意的x1,x2在[2,
]上恒成立,则(x1+x2)-1≤m≤(x1+x2)+1恒成立,进而可得实数m的取值范围.
(2)结合函数y=|f(x)|的图象和性质,由[-1,0]上单调递减,分类讨论满足条件的实数m的取值范围,最后综合讨论结果,可得答案;
(3)若对于区间[2,
| 5 |
| 2 |
| 5 |
| 2 |
解答:
解:(1)若函数y=lgf(x)在[2,4]上有意义,
则x2-mx+m-1>0,对任意的x∈[2,4]恒成立,
即m(x-1)<x2-1对任意的x∈[2,4]恒成立,
即m<x+1对任意的x∈[2,4]恒成立,
∴m<3
故实数m的取值范围(-∞,3)…(5分)
(2)令x2-mx+m-1=0,解得x=1或x=m-1
当m-1≥1,即m≥2时,函数f(x)在[-1,0]上恒非负且减,满足条件;
当m-1<1,即m<2时,若函数y=|f(x)|在[-1,0]上单调递减,
则m-1≥0或
≤-1
解得m≤-2
综上所述:m≤-2或m≥1
故实数m的取值范围(-∞,-2]∪[1,+∞)…(10分)
(3)若对于区间[2,
]内任意两个相异实数x1,x2,
且f(x1)-f(x2)=(x1-x2)(x1+x2-m)|(x1-x2)(x1+x2-m)|≤|x1-x2|(x1≠x2)恒成立,…12分
则|m-(x1+x2)|≤1对任意的x1,x2在[2,
]上恒成立.
则(x1+x2)-1≤m≤(x1+x2)+1恒成立…(14分)
∴4≤m≤5
故实数m的取值范围为[4,5]…(16分)
则x2-mx+m-1>0,对任意的x∈[2,4]恒成立,
即m(x-1)<x2-1对任意的x∈[2,4]恒成立,
即m<x+1对任意的x∈[2,4]恒成立,
∴m<3
故实数m的取值范围(-∞,3)…(5分)
(2)令x2-mx+m-1=0,解得x=1或x=m-1
当m-1≥1,即m≥2时,函数f(x)在[-1,0]上恒非负且减,满足条件;
当m-1<1,即m<2时,若函数y=|f(x)|在[-1,0]上单调递减,
则m-1≥0或
| m |
| 2 |
解得m≤-2
综上所述:m≤-2或m≥1
故实数m的取值范围(-∞,-2]∪[1,+∞)…(10分)
(3)若对于区间[2,
| 5 |
| 2 |
且f(x1)-f(x2)=(x1-x2)(x1+x2-m)|(x1-x2)(x1+x2-m)|≤|x1-x2|(x1≠x2)恒成立,…12分
则|m-(x1+x2)|≤1对任意的x1,x2在[2,
| 5 |
| 2 |
则(x1+x2)-1≤m≤(x1+x2)+1恒成立…(14分)
∴4≤m≤5
故实数m的取值范围为[4,5]…(16分)
点评:本题考查的知识点是二次函数的图象和性质,函数图象的对折变换,恒成立问题,是函数图象和性质的综合应用,难度较大.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
集合A={x|(x-1)(2x-3)≤1},B={x|-1<x<
},则A∩B为( )
| 3 |
| 2 |
A、{x|
| ||||
B、{x|1<x≤
| ||||
C、{x|
| ||||
D、{x|
|
已知集合A={1,2},B={1,a,b},则“a=2”是“A⊆B”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若点(x,y)位于曲线y=2|x|与y=2所围成的封闭区域,则2x-y的最小值为( )
| A、-4 | B、-6 | C、0 | D、1 |
 已知椭圆
已知椭圆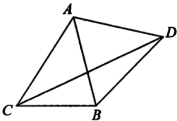 如图,△ABC中.角A、B、C所对边的长分别为a、b、c满足c=l,a2+b2=ab+1,以AB为边向△ABC外作等边三角形△ABD.
如图,△ABC中.角A、B、C所对边的长分别为a、b、c满足c=l,a2+b2=ab+1,以AB为边向△ABC外作等边三角形△ABD.