题目内容
下列命题中的真命题是( )
| A、若a>b>0,a>c,则a2>bc | ||||
B、若a>b>c,则
| ||||
| C、若a>b,n∈N*,则an>bn | ||||
| D、若a>b>0,则1na<1nb |
考点:命题的真假判断与应用,不等式的综合
专题:不等式
分析:A不等式两边同乘以一个正数,不等号的方向不变,所以A是正确的;
B当不等式两边同乘以一个负数时,不等号的方向要改变,这里c题目中没指出是正数、负数带是0,所以B是错误的;
C没有考虑到,不等式性质成立的条件,a>b>0,所以C是错误的;
D因为f(x)=lnx在定义域内是增函数,所以D是错误的.
B当不等式两边同乘以一个负数时,不等号的方向要改变,这里c题目中没指出是正数、负数带是0,所以B是错误的;
C没有考虑到,不等式性质成立的条件,a>b>0,所以C是错误的;
D因为f(x)=lnx在定义域内是增函数,所以D是错误的.
解答:
解:A、∵a>c且b>0,∴ab>bc,又∵a>b且a>0,∴a2>ab,∴a2>bc,A正确;
B、∵a>b,当c>0时,有
>
,当c<0时,有
<
,B错误;
C、取a=2,b=-2,n=2时有,22=(-2)2,∴an>bn不对;当a>b>0,n∈N*,有an>bn,C错误;
D、∵f(x)=lnx是增函数,∴当a>b>0,有1na>1nb,D错误.
故选:A.
B、∵a>b,当c>0时,有
| a |
| c |
| b |
| c |
| a |
| c |
| b |
| c |
C、取a=2,b=-2,n=2时有,22=(-2)2,∴an>bn不对;当a>b>0,n∈N*,有an>bn,C错误;
D、∵f(x)=lnx是增函数,∴当a>b>0,有1na>1nb,D错误.
故选:A.
点评:这题考查了不等式的一些基本性质,撑握好不等式性质,以及不等式成立的条件是做对这类题目的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
直线x=ky+3与双曲线
-
=1只有一个公共点,则k的值有( )
| x2 |
| 9 |
| y2 |
| 4 |
| A、1个 | B、2个 |
| C、3个 | D、无数多个 |
集合A={x|(x-1)(2x-3)≤1},B={x|-1<x<
},则A∩B为( )
| 3 |
| 2 |
A、{x|
| ||||
B、{x|1<x≤
| ||||
C、{x|
| ||||
D、{x|
|
已知集合A={1,2},B={1,a,b},则“a=2”是“A⊆B”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
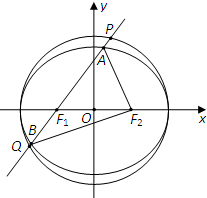 已知椭圆
已知椭圆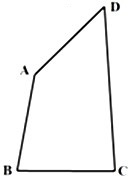 如图,在凸四边形ABCD中,C,D为定点,CD=
如图,在凸四边形ABCD中,C,D为定点,CD=