题目内容
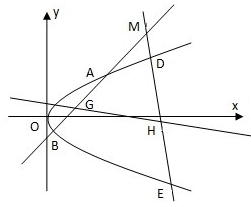 已知抛物线C:y2=2px(p>0),M点的坐标为(12,8),N点在抛物线C上,且满足
已知抛物线C:y2=2px(p>0),M点的坐标为(12,8),N点在抛物线C上,且满足| ON |
| 3 |
| 4 |
| OM |
(Ⅰ)求抛物线C的方程;
(Ⅱ)过点M作倾斜角互补的两条直线l1,l2,l1与抛物线C交于不同两点A,B,l2与抛物线C交于不同两点D,E,弦AB,DE的中点分别为G,H.求当直线l1的倾斜角在[
| π |
| 6 |
| π |
| 4 |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)由
=
,M点的坐标为(12,8),得出
=(9,6)代入y2=2px,求出p的值,即可求抛物线C的方程;
(Ⅱ)设l1斜率为k,方程为y=k(x-12)+8,则l2方程为y=-k(x-12)+8与y2=4x联立,求出G,H的坐标,可得GH的方程,代入抛物线方程,求出弦长PQ,即可求出直线GH被抛物线截得的弦长的最大值.
| ON |
| 3 |
| 4 |
| OM |
| ON |
(Ⅱ)设l1斜率为k,方程为y=k(x-12)+8,则l2方程为y=-k(x-12)+8与y2=4x联立,求出G,H的坐标,可得GH的方程,代入抛物线方程,求出弦长PQ,即可求出直线GH被抛物线截得的弦长的最大值.
解答:
解:(I)由
=
,M点的坐标为(12,8),得出
=(9,6)代入y2=2px,得到2p=4,
所以抛物线C的方程为y2=4x…(4分)
(II)由题意知直线l1,l2的斜率存在,且不为零,设l1斜率为k,方程为y=k(x-12)+8,
则l2方程为y=-k(x-12)+8
由y=k(x-12)+8与y2=4x联立,得:ky2-4y+32-48k=0…(5分)
△=16-4k(32-48k)>0,∴k>
或k<
.
设A(x1,y1),B(x2,y2),中点G(xG,yG),则y1+y2=
,即yG=
…(7分)
又yG=k(xG-12)+8,∴xG=
-
+12
∴G的坐标为(
-
+12,
).
用-k代替k,同理得-k>
或-k<
,H的坐标(
+
+12,-
).
∴k>
或-
<k<0,0<k<
.或k<-
,
又∵直线l1的倾斜角在[
,
],即
≤k≤1…(9分)
而kGH=
=-
∴GH:y=-
(x-xG)+yG,…(11分)
代入抛物线方程得:y2+16y-4(xG+4yG)=0
△=162+16(xG+4yG)=16(16+
+12)>0
设直线GH与抛物线C交于P,Q两点,
则弦长|PQ|=4
•
…(13分)
∵
≤k2≤1,∴1≤
≤3,
∴|PQ|max=68
∴直线GH被抛物线截得的弦长的最大值为68
.…(15分)
| ON |
| 3 |
| 4 |
| OM |
| ON |
所以抛物线C的方程为y2=4x…(4分)
(II)由题意知直线l1,l2的斜率存在,且不为零,设l1斜率为k,方程为y=k(x-12)+8,
则l2方程为y=-k(x-12)+8
由y=k(x-12)+8与y2=4x联立,得:ky2-4y+32-48k=0…(5分)
△=16-4k(32-48k)>0,∴k>
| 1 |
| 2 |
| 1 |
| 6 |
设A(x1,y1),B(x2,y2),中点G(xG,yG),则y1+y2=
| 4 |
| k |
| 2 |
| k |
又yG=k(xG-12)+8,∴xG=
| 2 |
| k2 |
| 8 |
| k |
∴G的坐标为(
| 2 |
| k2 |
| 8 |
| k |
| 2 |
| k |
用-k代替k,同理得-k>
| 1 |
| 2 |
| 1 |
| 6 |
| 2 |
| k2 |
| 8 |
| k |
| 2 |
| k |
∴k>
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 2 |
又∵直线l1的倾斜角在[
| π |
| 6 |
| π |
| 4 |
| ||
| 3 |
而kGH=
| ||||
-
|
| 1 |
| 4 |
∴GH:y=-
| 1 |
| 4 |
代入抛物线方程得:y2+16y-4(xG+4yG)=0
△=162+16(xG+4yG)=16(16+
| 2 |
| k2 |
设直线GH与抛物线C交于P,Q两点,
则弦长|PQ|=4
| 17 |
28+
|
∵
| 1 |
| 3 |
| 1 |
| k2 |
∴|PQ|max=68
| 2 |
∴直线GH被抛物线截得的弦长的最大值为68
| 2 |
点评:本题考查抛物线方程,考查直线与抛物线的位置关系,考查向量知识的运用,考查韦达定理,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
集合A={x|(x-1)(2x-3)≤1},B={x|-1<x<
},则A∩B为( )
| 3 |
| 2 |
A、{x|
| ||||
B、{x|1<x≤
| ||||
C、{x|
| ||||
D、{x|
|
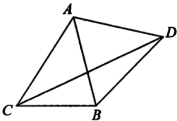 如图,△ABC中.角A、B、C所对边的长分别为a、b、c满足c=l,a2+b2=ab+1,以AB为边向△ABC外作等边三角形△ABD.
如图,△ABC中.角A、B、C所对边的长分别为a、b、c满足c=l,a2+b2=ab+1,以AB为边向△ABC外作等边三角形△ABD.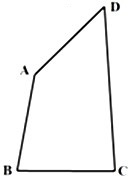 如图,在凸四边形ABCD中,C,D为定点,CD=
如图,在凸四边形ABCD中,C,D为定点,CD=