题目内容
11.在直角坐标系xoy中,曲线C1的参数方程为$\left\{\begin{array}{l}{x=\frac{2}{ta{n}^{2}α}}\\{y=\frac{2}{tanα}}\end{array}\right.$(α为参数,α≠$\frac{kπ}{2}$,k∈z),M是C1上的动点,P点满足$\overrightarrow{OP}$=$\frac{1}{2}$$\overrightarrow{OM}$,P点的轨迹为曲线C2.在以O为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程是ρsin(θ-$\frac{π}{4}$)+$\sqrt{2}$=0,直线l与曲线C2相交于A、B.(1)求曲线C1、C2的普通方程;
(2)求△ABO的面积.
分析 (1)由已知得$ta{n}^{2}α=\frac{4}{{y}^{2}}$,代入$x=\frac{2}{ta{n}^{2}α}$,能求出曲线C1的普通方程,设P(x,y),推导出M(2x,2y),由此能求出C2的普通方程.
(2)法一:由$\left\{\begin{array}{l}ρsin(θ-\frac{π}{4})+\sqrt{2}=0\\ ρ{sin^2}θ=cosθ\end{array}\right.$,得ρsinθ=2,或ρsinθ=-1,由此利用S△ABO=S△ACO+S△BCO能求出△ABO的面积.
法二:直线$l:ρsin(θ-\frac{π}{4})+\sqrt{2}=0$的直角坐标方程为x-y-2=0,联立$\left\{{\begin{array}{l}{{y^2}=x}\\{x-y-2=0}\end{array}}\right.$,得y2-y-2=0,由此能求出△ABO的面积.
解答 解:(1)∵曲线C1的参数方程为$\left\{\begin{array}{l}{x=\frac{2}{ta{n}^{2}α}}\\{y=\frac{2}{tanα}}\end{array}\right.$(α为参数,α≠$\frac{kπ}{2}$,k∈z),
∴${y}^{2}=\frac{4}{ta{n}^{2}α}$,∴$ta{n}^{2}α=\frac{4}{{y}^{2}}$,代入$x=\frac{2}{ta{n}^{2}α}$,
化简得曲线C1的普通方程:y2=2x,…(1分)
设P(x,y),P点满足$\overrightarrow{OP}$=$\frac{1}{2}$$\overrightarrow{OM}$,得M(2x,2y),…(3分)
∵M是C1上的动点,∴(2y)2=2(2x)…(4分)
∴y2=x,即C2的普通方程为y2=x(x>0)…(5分)
(2)解法一:在极坐标系中,直线$l:ρsin(θ-\frac{π}{4})+\sqrt{2}=0$与极轴相交于C(2,0),…(6分)
曲线C2的极坐标方程是ρsin2θ=cosθ(ρ≠0),…(7分)
由$\left\{\begin{array}{l}ρsin(θ-\frac{π}{4})+\sqrt{2}=0\\ ρ{sin^2}θ=cosθ\end{array}\right.$,得ρsinθ=2,或ρsinθ=-1…(8分)
设A(ρ1,θ1),B(ρ2,θ2),
∴${S_{△ABO}}={S_{△ACO}}+{S_{△BCO}}=\frac{1}{2}×2×|{ρ_1}sin{θ_1}|+\frac{1}{2}×2×|{ρ_2}sin{θ_2}|=3$…(10分)
解法二:直线$l:ρsin(θ-\frac{π}{4})+\sqrt{2}=0$的直角坐标方程为x-y-2=0…(6分)
且l与x轴交于D(2,0)…(7分);
联立$\left\{{\begin{array}{l}{{y^2}=x}\\{x-y-2=0}\end{array}}\right.$,消元得y2-y-2=0,…(8分);
设A(x1,y1)、B(x2,y2),则y1+y2=1,y1•y2=-2…(9分)
△ABO的面积S△ABO=$\frac{1}{2}•OD•$|y1-y2|=$\frac{1}{2}•2•\sqrt{1+8}$=3…(10分).
点评 本题考查曲线的普通方程的求法,考查三角形面积的求法,是中档题,解题时要认真审题,注意极坐标和直角坐标互化公式的合理运用.

| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
| A. | 24 | B. | 22 | C. | 18 | D. | 12 |
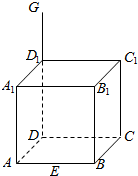 如图,G是正方体ABCD-A1B1C1D1的棱DD1延长线上的一点,E、F是棱AB、BC的中点,试分别画出过下列各点、直线的平面与正方体表面的交线.
如图,G是正方体ABCD-A1B1C1D1的棱DD1延长线上的一点,E、F是棱AB、BC的中点,试分别画出过下列各点、直线的平面与正方体表面的交线.