题目内容
19.设P={x||x-2|<3},Q={x|x2-x≥2},求P∩Q,P∪Q(用区间表示).分析 根据题意,P为绝对值值不等式的解集,解不等式可得集合P;Q为一元一次不等式的解集,解不等式可得集合Q,又由交集和并集的性质,计算可得答案
解答 解:∵P={x||x-2|<3}=(-1,5),
Q={x|x2-x≥2}=(-∞,-1]∪[2,+∞),
∴P∩Q=[2,5),
P∪Q=(-∞,+∞).
点评 本题考查集合的交集并集及其运算,解题时要认真审题,属于基础题.

练习册系列答案
相关题目
14.已知集合A={x|3≤x≤9},集合B={x|0<x<10},则集合A与B的关系是( )
| A. | A⊆B | B. | A?B | C. | B?A | D. | 以上均不对 |
8.方程y=$\sqrt{36-{x}^{2}}$表示的曲线是( )
| A. | 一个圆 | B. | 两条射线 | C. | 半个圆 | D. | 一条射线 |
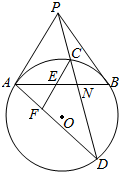 过圆外一点P向圆O作切线PA、PB及及割线PCD,过C作PA的平行线,分别交AB、AD与于E、F.求证:CE=EF.
过圆外一点P向圆O作切线PA、PB及及割线PCD,过C作PA的平行线,分别交AB、AD与于E、F.求证:CE=EF.