题目内容
8．正三角形ABC的两个顶点A，B在抛物线x2=2py（p＞0）上，另一个顶点C是此抛物线焦点，则满足条件的三角形ABC的个数为（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 由题意可知：x2=2py（P＞0）的焦点F（0，$\frac{p}{2}$），则两个边的斜率k=±tan60°=±$\sqrt{3}$，其方程为：y=±$\sqrt{3}$x+$\frac{p}{2}$，每条直线与抛物线均有两个交点，焦点两侧的两交点连接，分别构成一个等边三角形．满足条件的三角形ABC的个数为2，
解答 解：由抛物线x2=2py（P＞0）的焦点F（0，$\frac{p}{2}$），
等边三角形的一个顶点位于抛物线x2=2py（P＞0）的焦点，另外两个顶点在抛物线上，则等边三角形关于x轴轴对称
两个边的斜率k=±tan60°=±$\sqrt{3}$，其方程为：y=±$\sqrt{3}$x+$\frac{p}{2}$，
每条直线与抛物线均有两个交点，焦点两侧的两交点连接，分别构成一个等边三角形．
满足条件的三角形ABC的个数为2，
故选C．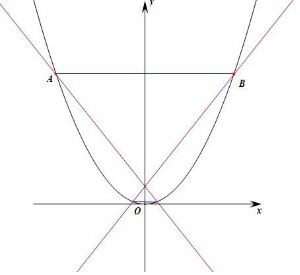
点评 本题主要考查了抛物线的简单性质．主要是利用抛物线和正三角形的对称性，考查数形结合思想，属于基础题．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
19．某班5名学生的数学和物理成绩如下表：
（1）求物理成绩y对数学成绩x的回归直线方程；
（2）一名学生的数学成绩是96，试预测他的物理成绩．
附：回归直线的斜率和截距的最小二乘法估计公式分别为：$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．
| A | B | C | D | E | |
| 数学成绩（x） | 88 | 76 | 73 | 66 | 63 |
| 物理成绩（y） | 78 | 65 | 71 | 64 | 61 |
（2）一名学生的数学成绩是96，试预测他的物理成绩．
附：回归直线的斜率和截距的最小二乘法估计公式分别为：$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．
16．现有编号为A，B，C，D的四本书，将这4本书平均分给甲、乙两位同学，则A，B两本书不被同一位同学分到的概率为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{2}$ |
3．已知抛物线y2=2px（p＞0）的焦点为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点，且其准线被该双曲线截得的弦长是$\frac{2}{3}$b，则该双曲线的离心率为（ ）
| A． | $\frac{13}{9}$ | B． | $\frac{10}{9}$ | C． | $\frac{\sqrt{13}}{3}$ | D． | $\frac{\sqrt{10}}{3}$ |
13．设集合A={x|-2≤x≤4}，B={x|x2-3x＞0}，则A∩B=（ ）
| A． | {x|-2≤x＜0或3＜x≤4} | B． | {x|-2≤x≤0或3≤x≤4} | C． | {x|-2＜x≤4} | D． | {x|0＜x＜3} |
20．已知集合A={x|log2（4-x）＜1}，B={x|3x-1≤9}，则A∩B=（ ）
| A． | （2，3） | B． | （2，4） | C． | （2，3] | D． | [2，3] |
17．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{12}=1（{a＞0}）$，以原点为圆心，双曲线的实轴长为半径长的圆与双曲线的两条渐近线相交于A，B，C，D四点，四边形的ABCD的面积为$2\sqrt{3}a$，则a的值为（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$或$2\sqrt{2}$ | D． | 2 |