题目内容
18.函数f(x)=log${\;}_{\frac{1}{2}}$(ax2-2x+4)(a∈R),若f(x)的值域为(-∞,1],则a的值为$\frac{2}{7}$.分析 根据对数的性质可知ax2-2x+4>0,函数y=ax2-2x+4的最小值为1.可得a的值.
解答 解:由题意,函数f(x)=log${\;}_{\frac{1}{2}}$(ax2-2x+4)
∵f(x)的值域为(-∞,1],
∴ax2-2x+4>0,函数y=ax2-2x+4的最小值为$\frac{1}{2}$,
即$\left\{\begin{array}{l}{a>0}\\{4×4a-(-2)^{2}=2a}\end{array}\right.$,
可得:a=$\frac{2}{7}$.
故答案为:$\frac{2}{7}$.
点评 本题考查了对数函数的运用和性质以及复合函数的值域问题.属于基础题.

练习册系列答案
相关题目
9.大前提:若函数f(x)是奇函数,则f(0)=0,小前提:$g(x)=\frac{1}{x}$是奇函数,结论:g(0)=0,则该推理过程( )
| A. | 正确 | B. | 因大前提错误导致结论出错 | ||
| C. | 因小前提导致结论出错 | D. | 因推理形式错误导致结论出错 |
13.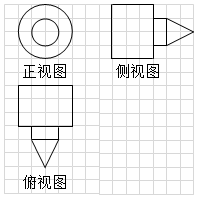 放烟花是逢年过节一种传统庆祝节日的方式.已知一种烟花模型的三视图如图中的粗实线所示,网格纸上小正方形的边长为1,则该烟花模型的表面积为(
放烟花是逢年过节一种传统庆祝节日的方式.已知一种烟花模型的三视图如图中的粗实线所示,网格纸上小正方形的边长为1,则该烟花模型的表面积为(
 放烟花是逢年过节一种传统庆祝节日的方式.已知一种烟花模型的三视图如图中的粗实线所示,网格纸上小正方形的边长为1,则该烟花模型的表面积为(
放烟花是逢年过节一种传统庆祝节日的方式.已知一种烟花模型的三视图如图中的粗实线所示,网格纸上小正方形的边长为1,则该烟花模型的表面积为(| A. | $(18+\sqrt{3})π$ | B. | $(21+\sqrt{3})π$ | C. | $(18+\sqrt{5})π$ | D. | $(21+\sqrt{5})π$ |
10.定义在R上的奇函数f(x)对任意x1,x2(x1≠x2)都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}>0$,若实数m,n满足f(m2+4m+12)+f(n2-6n)<0,则|m-2n-4|的取值范围为( )
| A. | $[\frac{{12\sqrt{5}}}{5}-1,\frac{{12\sqrt{5}}}{5}+1]$ | B. | $(\frac{{12\sqrt{5}}}{5}-1,\frac{{12\sqrt{5}}}{5}+1)$ | C. | $[12-\sqrt{5},12+\sqrt{5}]$ | D. | $(12-\sqrt{5},12+\sqrt{5})$ |