题目内容
11．在游乐场，有一种游戏是向一个画满均匀方格的桌面上投硬币，若硬币恰落在任何一个方格内不与方格线重叠，即可获奖．已知硬币的直径为2，若游客获奖的概率不超过$\frac{1}{9}$，则方格边长最长为（单位：cm）（ ）| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
分析 由题意知本题是一个几何概型，概率等于对应面积之比，根据题意算出试验包含的总面积和符合条件的面积，求比值即可．
解答 解：设小方格边长为acm，
∵硬币的直径为2cm，显然a≥2；
使硬币与小方格的四边不相交，则
这时硬币所在的位置可以是以方格中心为中心点，以a-2为边长的方格；
且与小方格的四边不相交的概率不超过$\frac{1}{9}$，
即p=$\frac{{（a-2）}^{2}}{{a}^{2}}$≤$\frac{1}{9}$，
解出$\frac{3}{2}$≤a≤3，
即a的取值范围为[2，3]满足条件；
∴方格边长最长为3．
故选：A．
点评 本题考查了几何概型和面积的计算问题，是基础题目．
练习册系列答案
相关题目
16．若x，y是正数，且$\frac{1}{x}$+$\frac{4}{y}$=1，则xy有（ ）
| A． | 最小值16 | B． | 最小值$\frac{1}{16}$ | C． | 最大值16 | D． | 最大值$\frac{1}{16}$ |
20．
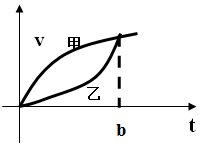甲、乙速度v与时间t的关系如图，a（b）是t=b时的加速度，S（b）是从t=0到t=b的路程，则a甲（b）与a乙（b），S甲（b）与S乙（b）的大小关系是（ ）
甲、乙速度v与时间t的关系如图，a（b）是t=b时的加速度，S（b）是从t=0到t=b的路程，则a甲（b）与a乙（b），S甲（b）与S乙（b）的大小关系是（ ）| A． | a甲（b）＞a乙（b），S甲（b）＞S乙（b） | B． | a甲（b）＜a乙（b），S甲（b）＜S乙（b） | ||
| C． | a甲（b）＜a乙（b），S甲（b）＞S乙（b） | D． | a甲（b）＜a乙（b），S甲（b）＜S乙（b） |