题目内容
16.若x,y是正数,且$\frac{1}{x}$+$\frac{4}{y}$=1,则xy有( )| A. | 最小值16 | B. | 最小值$\frac{1}{16}$ | C. | 最大值16 | D. | 最大值$\frac{1}{16}$ |
分析 利用基本不等式的性质即可得出.
解答 解:∵x>0,y>0,
∴1=$\frac{1}{x}+\frac{4}{y}$≥2$\sqrt{\frac{4}{xy}}$=4$\sqrt{\frac{1}{xy}}$,当且仅当4x=y=8时取等号.
∴$\frac{1}{4}≥\sqrt{\frac{1}{xy}}$,
即xy≥16,
∴xy有最小值为16.
故选A.
点评 本题考查了基本不等式的性质的运用,属于基础题.

练习册系列答案
相关题目
6.设角α的终边经过点(-6t,-8t) (t≠0),则sin α-cos α的值是( )
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | ±$\frac{1}{5}$ | D. | 不确定 |
1.不等式$\frac{2-x}{x+4}$>1的解集是( )
| A. | (-∞,-1) | B. | (-4,2) | C. | (-4,-1) | D. | (-4,+∞) |
8.当变量x,y满足约束条件$\left\{\begin{array}{l}y≥x\\ x+3y≤4\\ x≥m\end{array}\right.时,z=x-3y$的最大值为8,则实数m的值是-4.
5.甲、乙两人下棋,和棋的概率为$\frac{1}{2}$,乙获胜的概率为$\frac{1}{3}$,则甲获胜的概率和甲不输的概率分别为( )
| A. | $\frac{1}{6}$,$\frac{1}{6}$ | B. | $\frac{1}{2}$,$\frac{2}{3}$ | C. | $\frac{1}{6}$,$\frac{2}{3}$ | D. | $\frac{2}{3}$,$\frac{1}{2}$ |
6.偶函数f(x)(x∈R)满足:f(-5)=f(2),且在区间[0,3]与[3,+∞)上分别递减和递增,则不等式x•f(x)<0的解集为( )
| A. | (-∞,-5)∪(5,+∞) | B. | (-5,-2)∪(2,5) | C. | (-∞,-5)∪(-2,0) | D. | (-∞,-5)∪(-2,0)∪(2,5) |
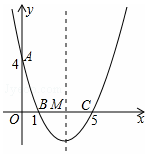 如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x 轴相交于点M.
如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x 轴相交于点M.