题目内容
19.圆柱OO1的高等于4cm,侧面积为16πcm2,AA1、BB1是圆柱的两条母线,它们之间的距离是2$\sqrt{3}$cm,M是BB1的中点,求A、M两点在圆柱侧面上连线的最小值.分析 求出展开图中,AB=$\frac{4π}{3}$,即可求出A、M两点在圆柱侧面上连线的最小值.
解答 解:由题意,圆柱底面圆的半径为2,
∵AA1、BB1是圆柱的两条母线,它们之间的距离是2$\sqrt{3}$cm,
∴弦心距为1,
∴弧AB所对的圆心角为120°,
∴展开图中,AB=$\frac{4π}{3}$,
∴A、M两点在圆柱侧面上连线的最小值=$\sqrt{4+\frac{16{π}^{2}}{9}}$.
点评 注意求曲面上两点间的最短距离时,一定要把它展开到一个平面上进行计算.

练习册系列答案
相关题目
14.等差数列{an}和{bn},{bn}的前n项和分别为Sn与Tn,对一切自然数n,都有$\frac{{S}_{n}}{{T}_{n}}$=$\frac{n}{n+1}$,则$\frac{{a}_{5}}{{b}_{5}}$等于( )?
| A. | $\frac{3}{4}$ | B. | $\frac{5}{6}$ | C. | $\frac{9}{10}$ | D. | $\frac{10}{11}$ |
8.当变量x,y满足约束条件$\left\{\begin{array}{l}y≥x\\ x+3y≤4\\ x≥m\end{array}\right.时,z=x-3y$的最大值为8,则实数m的值是-4.
9.某医院一天内派医生下乡医疗,派出医生数及概率如下:
求(1)派出医生为3人的概率;
(2)派出医生至多2人的概率.
(3)派出医生至少2 人的概率.
| 医生人数 | 0 | 1 | 2 | 3 | 4 | 5人以上 |
| 概率 | 0.1 | 0.16 | 0.2 | x | 0.2 | 0.04 |
(2)派出医生至多2人的概率.
(3)派出医生至少2 人的概率.
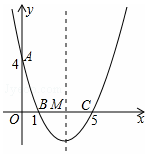 如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x 轴相交于点M.
如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x 轴相交于点M.