题目内容
假设关于某市的房屋面积x(平方米)与购房费用y(万元),有如下的统计数据:
(1)用最小二乘法求出y关于x的线性回归方程
=bx+a.
(2)在已有的四组数据中任意抽取两组,求恰有一组实际值小于预测值的概率.(参考数据:
xi2=36600,
xiyi=19290,线性回归方程的系数公式为b=
,a=
-b
)
| x(平方米) | 80 | 90 | 100 | 1l0 |
| y(万元) | 42 | 46 | 53 | 59 |
 |
| y |
(2)在已有的四组数据中任意抽取两组,求恰有一组实际值小于预测值的概率.(参考数据:
| n |
 |
| i=1 |
| n |
 |
| i=1 |
| |||||
|
. |
| y |
. |
| x |
考点:线性回归方程,古典概型及其概率计算公式
专题:计算题,概率与统计
分析:(1)根据统计数据,计算可得线性回归方程
=bx+a中系数a,b,代入公式即可求得线性回归方程;
(2)根据线性回归方程,可得预测值,再确定基本事件的个数,即可得出结论.
 |
| y |
(2)根据线性回归方程,可得预测值,再确定基本事件的个数,即可得出结论.
解答:
解:(1)
=
=95,
=
=50,
xi2=36600,
xiyi=19290,4
=19000,
2=36100
代入公式求得b=0.58,a=-5.1;
线性回归方程为
=0.58x-5.1;
(2)x=80时,
=35.3;x=90时,
=47.1;x=100时,
=53.1;x=110时,
=58.7,
已有的四组数据中任意抽取两组,共有
=6种,恰有一组实际值小于预测值,共有
=3种,
故概率为
=
.
. |
| x |
| 80+90+100+110 |
| 4 |
. |
| y |
| 42+46+53+59 |
| 4 |
| n |
 |
| i=1 |
| n |
 |
| i=1 |
. |
| x |
. |
| y |
. |
| x |
代入公式求得b=0.58,a=-5.1;
线性回归方程为
 |
| y |
(2)x=80时,
 |
| y |
 |
| y |
 |
| y |
 |
| y |
已有的四组数据中任意抽取两组,共有
| C | 2 4 |
| C | 1 3 |
故概率为
| 3 |
| 6 |
| 1 |
| 2 |
点评:本题考查线性回归方程,考查利用线性回归方程解决实际问题,正确运用公式是关键,属于中档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
设(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n,则a2+a4+…+a2n的值为( )
A、
| ||
B、
| ||
| C、3n-2 | ||
| D、3n |
 如图,PA为⊙O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5.求:
如图,PA为⊙O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5.求: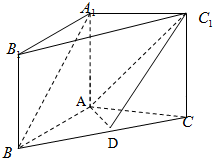 在三棱柱A1B1C1-ABC中,A1A⊥平面ABC,A1A=AB=AC=2,BC=2
在三棱柱A1B1C1-ABC中,A1A⊥平面ABC,A1A=AB=AC=2,BC=2