题目内容
设函数f(x)=x3-3x2-9x+a
(1)对于任意实数x,f′(x)≥m恒成立,求m的取值范围;
(2)若方程f(x)=0有且仅有一个实根,求a的取值范围.
(1)对于任意实数x,f′(x)≥m恒成立,求m的取值范围;
(2)若方程f(x)=0有且仅有一个实根,求a的取值范围.
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)由题意对于任意实数x,f′(x)≥m恒成立,即3x2-6x-9-m≥0恒成立,借助二次函数的图象性质,即可得出结论;
(2)转化为求函数的极值问题解决,利用导数解得函数的极值,即得结论.
(2)转化为求函数的极值问题解决,利用导数解得函数的极值,即得结论.
解答:
解:(1)f′(x)=3x2-6x-9=3(x-1)(x-3)
因为x∈(-∞,+∞),f′(x)≥m,即3x2-6x-9-m≥0恒成立,
所以△=36-12(-9-m)≤0,得m≤-12;
(2)因为当x<1时,f′(x)>0;当1<x<3时,f′(x)<0;当x>3时,f′(x)>0;
所以,当x=1时,f(x)取极大值f(1)=a-11;
当x=3时,f(x)取极小值f(3)=a-27;
故当f(3)>0 或f(1)<0时,方程f(x)=0仅有一个实根,
解得a<11或a>27.
因为x∈(-∞,+∞),f′(x)≥m,即3x2-6x-9-m≥0恒成立,
所以△=36-12(-9-m)≤0,得m≤-12;
(2)因为当x<1时,f′(x)>0;当1<x<3时,f′(x)<0;当x>3时,f′(x)>0;
所以,当x=1时,f(x)取极大值f(1)=a-11;
当x=3时,f(x)取极小值f(3)=a-27;
故当f(3)>0 或f(1)<0时,方程f(x)=0仅有一个实根,
解得a<11或a>27.
点评:本题主要考查二次函数的性质及恒成立问题、方程的根问题的处理策略,考查利用导数研究函数的极值的知识,属中档题.

练习册系列答案
相关题目
复数
在复平面内对应的点位于( )
| 1-i |
| 2+3i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
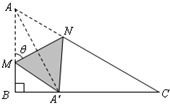 如图,直角三角形ABC中,∠B=90°,AB=1,BC=
如图,直角三角形ABC中,∠B=90°,AB=1,BC=

 如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,过C作圆的切线l,过A作l的垂线AD,垂足为D,则线段AE的长等于
如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,过C作圆的切线l,过A作l的垂线AD,垂足为D,则线段AE的长等于