题目内容
方程x2+2mx+2m+1=0在(-1,0)和(1,2)各有一个根,求m的取值范围.
考点:一元二次方程的根的分布与系数的关系
专题:函数的性质及应用
分析:令f(x)=x2+2mx+2m+1,由题意可得
,解不等式组求得m的取值范围.
|
解答:
解:令f(x)=x2+2mx+2m+1,∵方程x2+2mx+2m+1=0在(-1,0)和(1,2)各有一个根,∴
,
即
.
解得-
<m<-
,即 m的取值范围为(-
,-
).
|
即
|
解得-
| 5 |
| 6 |
| 1 |
| 2 |
| 5 |
| 6 |
| 1 |
| 2 |
点评:本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质,体现了转化的数学思想,属于中档题.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
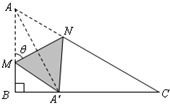 如图,直角三角形ABC中,∠B=90°,AB=1,BC=
如图,直角三角形ABC中,∠B=90°,AB=1,BC=

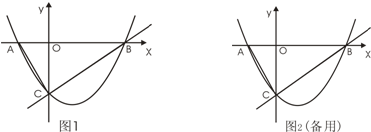
 如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,过C作圆的切线l,过A作l的垂线AD,垂足为D,则线段AE的长等于
如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,过C作圆的切线l,过A作l的垂线AD,垂足为D,则线段AE的长等于