题目内容
椭圆M:
+
=1(a>b>0)的离心率为
,且过点(
,
).
(1)求椭圆M的方程;
(2)直线l与椭圆M交于A,B两点,且线段AB的垂直平分线经过点(0,-
),求△AOB(O为原点)面积的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| 2 |
| ||
| 3 |
(1)求椭圆M的方程;
(2)直线l与椭圆M交于A,B两点,且线段AB的垂直平分线经过点(0,-
| 1 |
| 2 |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)依题意,椭圆M:
+
=1(a>b>0)的离心率为
,且过点(
,
),建立方程组,可求得a,b,从而可得椭圆M的方程;
(2)设A(x1,y1),B(x2,y2),依题意,直线AB有斜率,可分直线AB的斜率k=0与直线AB的斜率k≠0讨论,利用弦长公式,再结合基本不等式即可求得各自情况下S△AOB的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| 2 |
| ||
| 3 |
(2)设A(x1,y1),B(x2,y2),依题意,直线AB有斜率,可分直线AB的斜率k=0与直线AB的斜率k≠0讨论,利用弦长公式,再结合基本不等式即可求得各自情况下S△AOB的最大值.
解答:
解:(1)∵椭圆M:
+
=1(a>b>0)的离心率为
,且过点(
,
),
∴
,
∴a2=3,b2=1,
∴椭圆M的方程为
+y2=1;
(2)设A(x1,y1),B(x2,y2),则
∵AB的垂直平分线经过点(0,-
),显然直线AB有斜率,
当直线AB的斜率为0时,AB的垂直平分线为y轴,则x1=-x2,y1=y2,
∴S△AOB=
|2x1||y1|=|x1||y1|=
,
∵
≤
=
,
∴S△AOB≤
,当且仅不当|x1|=
时,S△AOB取得最大值为
;
当直线AB的斜率不为0时,则设AB的方程为y=kx+t,
与椭圆方程联立,得到(3k2+1)x2+6ktx+3t2-3=0,
当△=4(9k2+3-3t2)>0,即3k2+1>t2①,方程有两个不同的实数解;
又x1+x2=
,
∴
=-
∴
=
,
又
=-
,化简得到3k2+1=4t②
代入①,得到0<t<4,…10分
又原点到直线的距离为d=
,
|AB|=
|x1-x2|=
•
,
∴S△AOB=
|AB||d|=
•
•
•
=
∵0<t<4,所以当t=2时,即k=±
时,S△AOB取得最大值为
.
综上,S△AOB取得最大值为
.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| 2 |
| ||
| 3 |
∴
|
∴a2=3,b2=1,
∴椭圆M的方程为
| x2 |
| 3 |
(2)设A(x1,y1),B(x2,y2),则
∵AB的垂直平分线经过点(0,-
| 1 |
| 2 |
当直线AB的斜率为0时,AB的垂直平分线为y轴,则x1=-x2,y1=y2,
∴S△AOB=
| 1 |
| 2 |
|
∵
| x12(3-x12) |
| x12+(3-x12) |
| 2 |
| 3 |
| 2 |
∴S△AOB≤
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
当直线AB的斜率不为0时,则设AB的方程为y=kx+t,
与椭圆方程联立,得到(3k2+1)x2+6ktx+3t2-3=0,
当△=4(9k2+3-3t2)>0,即3k2+1>t2①,方程有两个不同的实数解;
又x1+x2=
| -6kt |
| 3k2+1 |
∴
| x1+x2 |
| 2 |
| 3kt |
| 3k2+1 |
∴
| y1+y2 |
| 2 |
| t |
| 3k2+1 |
又
| ||||
0-
|
| 1 |
| k |
代入①,得到0<t<4,…10分
又原点到直线的距离为d=
| |t| | ||
|
|AB|=
| 1+k2 |
| 1+k2 |
| ||
| 3k2+1 |
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| |t| | ||
|
| 1+k2 |
| ||
| 3k2+1 |
| 1 |
| 4 |
| 3(4t-t2) |
∵0<t<4,所以当t=2时,即k=±
|
| ||
| 2 |
综上,S△AOB取得最大值为
| ||
| 2 |
点评:本题考查椭圆的定义及其性质,椭圆方程的求法,直线与椭圆的位置关系,弦长公式的应用,直线方程以及韦达定理的应用.难度比较大,解题需要一定的运算能力以及分析问题解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=sin(2x+
)的图象是由函数y=sinx的图象经过,下列哪两次变换而得到的( )
| π |
| 3 |
A、先将y=sinx图象上各点的横坐标缩短到原来的一半,再将所得图象向左平移
| ||
B、先将y=sinx的图象上各点的横坐标伸长到原来的2倍,再将所得图象向左平衡
| ||
C、先将y=sinx的图象向左平移
| ||
D、先将y=sinx的图象向左平移
|
已知l,m,n是空间三条不同直线,命题p:若l⊥m,l⊥n,则m∥n;命题q:若三条直线l,m,n两两相交,则直线l,m,n共面,则下列命题为真命题的是( )
| A、p∧q | B、p∨q |
| C、p∨(¬q) | D、(¬p)∧q |
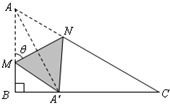 如图,直角三角形ABC中,∠B=90°,AB=1,BC=
如图,直角三角形ABC中,∠B=90°,AB=1,BC=
