题目内容
 已知三棱锥A-BCD,平面α与棱AC、BC、BP、AD分别交于M、N、P、Q.
已知三棱锥A-BCD,平面α与棱AC、BC、BP、AD分别交于M、N、P、Q.(1)若AB∥α,CD∥α,证明:四边形MNPQ为平行四边形;
(2)若四边形MNPQ为平行四边形,求证:AB∥α,CD∥α.
考点:直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)运用直线与平面平行的性质定理,平行四边形的定义判断即可.
(2)四边形MNPQ为平行四边形得出QM∥PN,MN∥PQ,再运用直线与平面平行的判断与性质证明即可.
(2)四边形MNPQ为平行四边形得出QM∥PN,MN∥PQ,再运用直线与平面平行的判断与性质证明即可.
解答:
证明:

(1)在三棱锥A-BCD,
平面α与棱AC、BC、BP、AD分别交于M、N、P、Q.
∵AB∥α,AB?面ACB,面ACB∩面MNPQ=MN
∴AB∥MN,
同理AB∥PQ,
即MN∥PQ,
∵CD∥α,CD?面ACD,面ACD∩面MNPQ=QM,
∴CD∥QM,
同理CD∥PN,
即QM∥PN,
∴四边形MNPQ为平行四边形;
(2)∵四边形MNPQ为平行四边形,
∴QM∥PN,MN∥PQ,
∵PN?面ADC,QM?面ADC,
∴PN∥面ADC,
∵PN?面BDC,面BDC∩面ADC=DC,
∴DC∥PN,
∵DC?面MNPQ,PN?面MNPQ,
∴CD∥面MNPQ,
即CD∥α.
同理:AB∥面MNPQ,
即:AB∥α

(1)在三棱锥A-BCD,
平面α与棱AC、BC、BP、AD分别交于M、N、P、Q.
∵AB∥α,AB?面ACB,面ACB∩面MNPQ=MN
∴AB∥MN,
同理AB∥PQ,
即MN∥PQ,
∵CD∥α,CD?面ACD,面ACD∩面MNPQ=QM,
∴CD∥QM,
同理CD∥PN,
即QM∥PN,
∴四边形MNPQ为平行四边形;
(2)∵四边形MNPQ为平行四边形,
∴QM∥PN,MN∥PQ,
∵PN?面ADC,QM?面ADC,
∴PN∥面ADC,
∵PN?面BDC,面BDC∩面ADC=DC,
∴DC∥PN,
∵DC?面MNPQ,PN?面MNPQ,
∴CD∥面MNPQ,
即CD∥α.
同理:AB∥面MNPQ,
即:AB∥α
点评:本题考察了直线与平面平行的性质,判定定理,平行四边形的性质,判定,综合考察了空间的线面的平行问题.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
椭圆
+
=1上有n个不同的点P1、P2、…、Pn,椭圆的右焦点为F,数列{|PnF|}是公差大于
的等差数列,则n的最大值是( )
| x2 |
| 4 |
| y3 |
| 3 |
| 1 |
| 1000 |
| A、2 000 |
| B、2 006 |
| C、2 007 |
| D、2 008 |
已知平面内一点P及△ABC,若
+
+
=
,则点P与△ABC的位置关系是( )
| PA |
| PB |
| PC |
| AB |
| A、点P在线段AB上 |
| B、点P在线段BC上 |
| C、点P在线段AC上 |
| D、点p在△ABC外部 |
设m,n表示不同直线,α,β表示不同平面,则下列命题中正确的是( )
| A、若m∥α,m∥n,则n∥α |
| B、若m?α,n?β,n∥α,则α∥β |
| C、若α∥β,m∥α,m∥n,则n∥β |
| D、若α∥β,m∥α,n∥m,n?β,则n∥β |
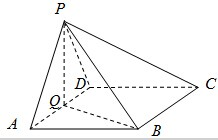 在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,若PA=PD.
在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,若PA=PD.