Question

已知直线3x+4y+5=0截圆C₁：x²+y²=r²所得弦长为6，M，N分别为椭圆C₂：

x2

a2

+

y2

b2

=1的左顶点和上顶点，C₂的离心率e=

2 3

3

，且|MN|等于圆C₁的半径．
（1）求C₁和C₂的方程；
（2）过圆上任一点P向圆C₂引两条切线，切点分别为A，B，判断∠APB是否为定值．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：计算题,作图题,圆锥曲线中的最值与范围问题

分析：（1）由题意求圆心到直线的距离，从而求半径，再由|MN|=

a2+b2

=

10

，e=

2 3

3

=

a

c

，及a²=b²+c²求C₂的方程；
（2）分直线的斜率是否存在讨论，不存在时可知为直角，故若为定值，则为直角，从而转化为证明斜率之积为-1即可，故设直线的方程为y-

10

sina=k（x-

10

cosa），与椭圆方程联立并令△=0，从而利用韦达定理可得．

解答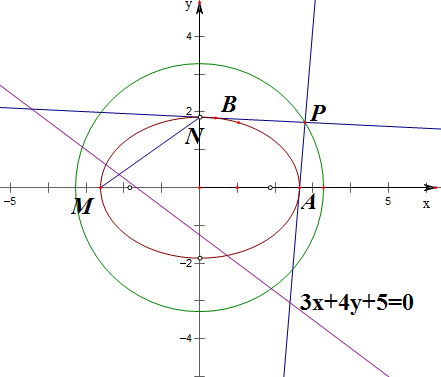： 解：（1）由题意，圆心到直线的距离d=

|5|

9+16

=1，
故r²=1²+3²=10，
故圆C₁：x²+y²=10，
由|MN|=

a2+b2

=

10

，e=

2 3

3

=

a

c

，及a²=b²+c²得，
a²=8，b²=2，c²=6，
故C₂的方程为

x2

8

+

y2

2

=1；
（2）设点P（

10

cosa，

10

sina），
若直线的斜率不存在时，即

10

cosa=±

8

时，

10

sina=±

2

，
故此时∠APB为直角，
若∠APB为定值，则∠APB为直角，
若直线的斜率存在，不妨设为k；
则直线的方程为y-

10

sina=k（x-

10

cosa），
与

x2

8

+

y2

2

=1联立消y可得，
2x²+8（

10

sina+k（x-

10

cosa））²-16=0，
即2（1+4k²）x²+16

10

k（sina-kcosa）x+80（sina-kcosa）²-16=0，
则△=[16

10

k（sina-kcosa）]²-4[2（1+4k²）][80（sina-kcosa）²-16]=0，
即4k²-5（sina-kcosa）²+1=0
即（4-5cos²a）k²+10ksinacosa+1-5sin²a=0，
则k₁•k₂=

1-5sin2a

4-5cos2a

=

cos2a-4sin2a

4sin2a-cos2a

=-1，
故∠APB为直角．
综上所述，∠APB为定值，且为直角．

点评：本题考查了圆锥曲线与直线的位置关系，同时考查了圆的方程与椭圆的方程的求法，难点在于确定判断∠APB是否为定值的方向，可先讨论特殊情况，从而转化为常见问题，属于难题．