题目内容
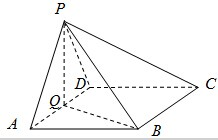在四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点，若PA=PD．（1）求证：平面PQB⊥平面PAD；
（2）若平面PAD⊥平面ABCD．求证：PQ⊥平面ABCD．
考点：平面与平面垂直的判定,直线与平面垂直的判定
专题：空间位置关系与距离
分析：（1）首先利用菱形的特殊的边角关系证得BQ⊥AD，进一步利用PA=PD，证得PQ⊥AD，进一步得到线面垂直，最后转化为面面垂直．
（2）直接利用面面垂直的性质定理，得到线面垂直．
（2）直接利用面面垂直的性质定理，得到线面垂直．
解答：
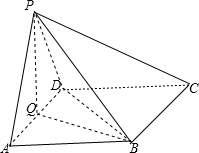证明：（1）在四棱锥P-ABCD中，连结BD，
因为：底面ABCD为菱形，∠BAD=60°，Q为AD的中点，
所以：BQ⊥AD，
又PA=PD，
所以：PQ⊥AD，
所以：AD⊥平面PQB，
AD?平面PAD，
平面PQB⊥平面PAD．
（2）已知平面PAD⊥平面ABCD，
PQ?平面PAD，平面PAD∩平面ABCD=AD，
且PQ⊥AD，
所以：PQ⊥平面ABCD．
证明：（1）在四棱锥P-ABCD中，连结BD，因为：底面ABCD为菱形，∠BAD=60°，Q为AD的中点，
所以：BQ⊥AD，
又PA=PD，
所以：PQ⊥AD，
所以：AD⊥平面PQB，
AD?平面PAD，
平面PQB⊥平面PAD．
（2）已知平面PAD⊥平面ABCD，
PQ?平面PAD，平面PAD∩平面ABCD=AD，
且PQ⊥AD，
所以：PQ⊥平面ABCD．
点评：本题考查的知识要点：线面垂直的判定与性质定理，面面垂直的性质定理，属于基础题型．
练习册系列答案
相关题目
已知三棱锥A-BCD，平面α与棱AC、BC、BP、AD分别交于M、N、P、Q．
在直三棱柱ABC-A′B′C′中，底面ABC是边长为2的正三角形，D′是棱A′C′的中点，且AA′=2