题目内容
12.过双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的焦点$F(2\sqrt{2},0)$作渐近线垂线,垂足为A若△OAF的面积为2(O为坐标原点),则双曲线离心率为$\sqrt{2}$.分析 S△OAF=2,运用三角形的面积公式,结合a,b,c的关系,解得a=b=2,即可得到双曲线离心率的值.
解答 解:在Rt△OAF中,$|{AF}|=c•sin∠AOF=c•\frac{b}{c}=b$,同理,|OA|=a,
∴${S_{△OAF}}=\frac{1}{2}|{OA}|•|{AF}|=\frac{1}{2}ab$,
又S△OAF=2,∴ab=4,而$c=2\sqrt{2}$,即a2+b2=8,∴a=b=2,∴$e=\sqrt{2}$.
故答案为$\sqrt{2}$.
点评 本题考查双曲线离心率的求法,考查三角形面积的计算,考查运算能力,属于基础题.

练习册系列答案
相关题目
3.在复平面内,复数$\frac{2-i}{1-i}$(i是虚数单位)对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.下列命题中正确的是( )
| A. | 若p∨q为真命题,则p∧q为真命题 | |
| B. | “x=5”是“x2-4x-5=0”的充分不必要条件 | |
| C. | 命题“若x<-1,则x2-2x-3>0”的否命题为:“若x<-1,则x2-2x-3≤0” | |
| D. | 已知命题p:?x∈R,x2+x-1<0,则¬p:?x∈R,x2+x-1≥0 |
7.一个几何体的三视图如图所示,则此几何体的体积为( )
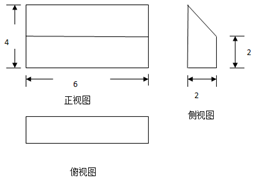

| A. | 16 | B. | 36 | C. | 48 | D. | 72 |
4.在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,PA=AB,E,F,H分别是棱PA,PB,AD的中点,且过E,F,H的平面截四棱锥P-ABCD所得截面面积为$\frac{{3\sqrt{2}}}{2}$,则四棱锥P-ABCD的体积为( )
| A. | $\frac{8}{3}$ | B. | 8 | C. | $8\sqrt{3}$ | D. | $24\sqrt{3}$ |
1.已知曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的渐近线方程为y=±$\frac{\sqrt{2}}{2}$x,则该曲线的离心率为( )
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\sqrt{3}$ |
2.定义在R上的函数y=f(x)在(-∞,a)上是增函数,函数y=f(x+a)是偶函数,当x1<x2且x1+x2>2a时,有( )
| A. | f(2a-x1)<f(2a-x2) | B. | f(2a-x1)>f(2a-x2) | C. | f(2a-x1)=f(2a-x2) | D. | 以上都不正确 |