题目内容
4．在四棱锥P-ABCD中，底面ABCD是正方形，PA⊥底面ABCD，PA=AB，E，F，H分别是棱PA，PB，AD的中点，且过E，F，H的平面截四棱锥P-ABCD所得截面面积为$\frac{{3\sqrt{2}}}{2}$，则四棱锥P-ABCD的体积为（ ）| A． | $\frac{8}{3}$ | B． | 8 | C． | $8\sqrt{3}$ | D． | $24\sqrt{3}$ |
分析 取BC中点M，连结FM，HM，推导出平面EFMH是过E，F，H的平面截四棱锥P-ABCD所得截面，设PA=AB=a，则S梯形EFMH=$\frac{1}{2}（\frac{a}{2}+a）×\frac{\sqrt{{a}^{2}+{a}^{2}}}{2}$=$\frac{3\sqrt{2}}{2}$，求出a=2，由此能求出四棱锥P-ABCD的体积．
解答 解：
取BC中点M，连结FM，HM，
∵在四棱锥P-ABCD中，底面ABCD是正方形，PA⊥底面ABCD，
PA=AB，E，F，H分别是棱PA，PB，AD的中点，
∴EF∥AB∥MH，∴EF⊥EH，MH⊥EH，
平面EFMH是过E，F，H的平面截四棱锥P-ABCD所得截面，
设PA=AB=a，
∵过E，F，H的平面截四棱锥P-ABCD所得截面面积为$\frac{{3\sqrt{2}}}{2}$，
∴S梯形EFMH=$\frac{1}{2}（EF+MH）×EH$=$\frac{1}{2}（\frac{a}{2}+a）×\frac{\sqrt{{a}^{2}+{a}^{2}}}{2}$=$\frac{3\sqrt{2}}{2}$，
解得a=2，
∴四棱锥P-ABCD的体积V=$\frac{1}{3}×{S}_{正方形ABCD}×SA$=$\frac{1}{3}×2×2×2$=$\frac{8}{3}$．
故选：A．
点评 本题考查柱、锥、台体的体积的求法，考查空间想象能力与计算能力，是中档题．
练习册系列答案
相关题目
如图，已知F1，F2是双曲线$C：\frac{x^2}{2}-\frac{y^2}{2}=1$的左，右焦点，点A在双曲线的右支上，线段AF1与双曲线左支相交于点B，△F2AB的内切圆与BF2相切于点E，若|AF2|=2|BF1|，则|BE|=$2\sqrt{2}$．
9．
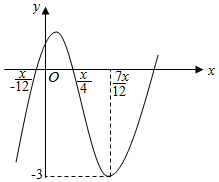已知函数f（x）=Asin（ωx+φ）+B（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，将函数f（x）的图象向左平移m（m＞0）个单位后，得到的图象关于点（$\frac{π}{6}$，-1）对称，则m的最小值是（ ）
已知函数f（x）=Asin（ωx+φ）+B（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，将函数f（x）的图象向左平移m（m＞0）个单位后，得到的图象关于点（$\frac{π}{6}$，-1）对称，则m的最小值是（ ）| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{5}{6}$π | D． | $\frac{2π}{3}$ |