题目内容

2．定义在R上的函数y=f（x）在（-∞，a）上是增函数，函数y=f（x+a）是偶函数，当x1＜x2且x1+x2＞2a时，有（　　）
A．f（2a-x1）＜f（2a-x2）B．f（2a-x1）＞f（2a-x2）C．f（2a-x1）=f（2a-x2）D．以上都不正确

分析 根据题意，分析可得，函数f（x）的图象关于直线x=a对称，且在区间（a，+∞）为减函数，再由x1＜x2且x1+x2＞2a，分析可得|x1-a|＜|x2-a|，我们分别判断2a-x1与2a-x2到函数图象对称轴的距离，即|a-（2a-x1）|，|a-（2a-x2）|的大小，再根据离对称轴近的函数值大，即可得到答案．

解答 解：根据题意，若函数y=f（x+a）是偶函数，则函数y=f（x）的图象关于直线x=a对称，
又由函数y=f（x）在（-∞，a）上是增函数，则其在区间（a，+∞）为减函数，
若x1＜x2且x1+x2＞2a，则有|x1-a|＜|x2-a|，
|a-（2a-x1）|=|x1-a|＜|a-（2a-x2）|=|x2-a|
∴f（2a-x1）＞f（2a-x2）；
故选：B．

点评 本题考查函数奇偶性的性质，涉及函数单调性的性质，其中根据已知条件，分析得到函数y=f（x）的图象关于直线x=a对称是解答本题的关键．

练习册系列答案
相关题目
12．过双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的焦点$F（2\sqrt{2}，0）$作渐近线垂线，垂足为A若△OAF的面积为2（O为坐标原点），则双曲线离心率为$\sqrt{2}$．
13．已知圆x2+y2=r2，直线l：y=x+$\sqrt{2}$，当圆上恰有三个点到直线l的距离都为1时，则r=2．
10．阅读如图的程序框图，运行相应的程序，则输出s的值为（　　）
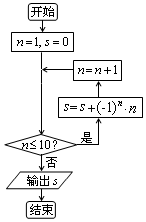
A．-6B．6C．-5D．5
17．若抛物线y2=2px的焦点与椭圆$\frac{x^2}{5}+{y^2}=1$的右焦点重合，则p=4．
7．某校高三（1）班全体女生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如图所示，据此解答如下问题：
（1）求分数在[80，90）内的女生人数，并计算频率分布直方图中[80，90）对应的矩形的高；
（2）以这个班的样本数据来估计全校的总体数据，若从全校高三女生中任选三人，设X表示数学成绩不低于80分的学生人数，求X的分布列和数学期望．
14．已知函数f（x）=x+1+|3-x|，x≥-1．
（I）求不等式f（x）≤6的解集；
（Ⅱ）若f（x）的最小值为n，正数a，b满足2nab=a+2b，求2a+b的最小值．
11．已知x、y满足$\left\{\begin{array}{l}{|x|≤1}\\{|x-y|≤1}\end{array}\right.$，则z=x+y+1的最大值为4．
12．已知函数f（x）=|x+a|+|x+$\frac{1}{a}$|（a＞0）（a＜0）
（1）当a=2时，求不等式f（x）＞3的解集
（2）证明：$f（m）+f（-\frac{1}{m}）≥4$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网