题目内容
17.已知函数f(x)=lnx+ax-x2(0<a≤1)(I)$a=\frac{1}{2}$时,求f(x)的图象在点(1,f(1))处的切线的方程
(II)设函数f(x)单调递增区间为(s,t)(s<t),求t-s的最大值.
分析 (I)利用导数的几何意义求出切线的斜率f′(1),再计算f(1),代入点斜式方程化简即可;
(II)令f′(x)>0可得2x2-ax-1<0,根据二次函数的性质及根与系数的关系可得s=0,t=$\frac{a+\sqrt{{a}^{2}+8}}{4}$,再利用函数单调性和a的范围得出t-s的最大值.
解答 解:(Ⅰ)∵$f'(x)=\frac{1}{x}+a-2x$,∴$f'(1)=a-1=-\frac{1}{2}$,
又$f(1)=a-1=-\frac{1}{2}$,
∴y=f(x)的图象在(1,f(1))处的切线方程为y+$\frac{1}{2}$=-$\frac{1}{2}$(x-1),即$y=-\frac{1}{2}x$.
(Ⅱ)$f'(x)=\frac{{1+ax-2{x^2}}}{x}\;({x>0})$,
令f′(x)>0得2x2-ax-1<0,
∵△=a2+8>0,∴2x2-ax-1=0有两根x1,x2(x1<x2),
又${x_1}{x_2}=-\frac{1}{2}<0$,
∴(s,t)=(0,x2),则$t-s={x_2}=\frac{{a+\sqrt{{a^2}+8}}}{4}$,
而$y=\frac{{a+\sqrt{{a^2}+8}}}{4}$在(0,1]上单调递增,
∴a=1时,$\frac{a+\sqrt{{a}^{2}+8}}{4}$取得最大值1,
∴a=1时t-s取得最大值1.
点评 本题考查了导数的几何意义,导数与函数单调性的关系,函数最值的计算,属于中档题.

练习册系列答案
相关题目
7.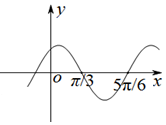 已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位,得到g(x)的图象,则函数g(x)的解析式为( )
已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位,得到g(x)的图象,则函数g(x)的解析式为( )
 已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位,得到g(x)的图象,则函数g(x)的解析式为( )
已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位,得到g(x)的图象,则函数g(x)的解析式为( )| A. | g(x)=sin2x | B. | g(x)=cos2x | C. | $g(x)=sin(2x+\frac{π}{6})$ | D. | $g(x)=sin(2x+\frac{2π}{3})$ |
8.已知复数$z=\frac{2+ai}{3-i}$是纯虚数(其中i为虚数单位,a∈R),则z的虚部为( )
| A. | 2 | B. | -2 | C. | 2i | D. | -2i |
2. 已知某几何体的三视图如图所示,则该几何体的体积为( )
已知某几何体的三视图如图所示,则该几何体的体积为( )
 已知某几何体的三视图如图所示,则该几何体的体积为( )
已知某几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{4}{3}$+π | B. | 4+π | C. | $\frac{4}{3}$+2π | D. | 4+2π |
9.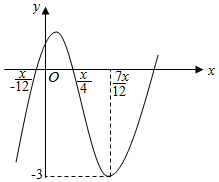 已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向左平移m(m>0)个单位后,得到的图象关于点($\frac{π}{6}$,-1)对称,则m的最小值是( )
已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向左平移m(m>0)个单位后,得到的图象关于点($\frac{π}{6}$,-1)对称,则m的最小值是( )
 已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向左平移m(m>0)个单位后,得到的图象关于点($\frac{π}{6}$,-1)对称,则m的最小值是( )
已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向左平移m(m>0)个单位后,得到的图象关于点($\frac{π}{6}$,-1)对称,则m的最小值是( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5}{6}$π | D. | $\frac{2π}{3}$ |