题目内容
（x2-4x+4）3的展开式中x的系数是 ．
考点：二项式系数的性质
专题：二项式定理
分析：把（x2-4x+4）3化为（x-2）6，利用二项式展开式的通项公式，求出展开式中x的系数即可．
解答：
解：∵（x2-4x+4）3=（x-2）2×3=（x-2）6，
∴二项式展开式的通项是
Tr+1=
•x6-r•（-2）r，
令6-r=1，
解得r=5；
∴
•（-2）5=6×（-32）=192，
即展开式中x的系数是192．
故答案为：192．
∴二项式展开式的通项是
Tr+1=
| C | r 6 |
令6-r=1，
解得r=5；
∴
| C | 5 6 |
即展开式中x的系数是192．
故答案为：192．
点评：本题考查了二项式展开式的通项公式的应用问题，是计算题目．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
某几何体的三视图如图所示，其中正视图和左视图的上半部分均为边长为2的等边三角形，则该几何体的体积为一个四棱锥的底面为正方形，其三视图如图所示，则这个四棱锥的侧面积是（ ）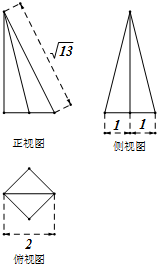
| A、2 | ||||
B、3
| ||||
C、3
| ||||
D、3
|