题目内容
7个排成一排,在下列情况下,各有多少种不同排法?
(1)甲排头;
(2)甲、乙、丙三人必须在一起;
(3)甲、乙、丙三人两两不相邻;
(4)甲不排头,乙不排当中.
(1)甲排头;
(2)甲、乙、丙三人必须在一起;
(3)甲、乙、丙三人两两不相邻;
(4)甲不排头,乙不排当中.
考点:计数原理的应用
专题:计算题,排列组合
分析:(1)甲固定不动,其余6人全排;
(2)甲、乙、丙三人必须在一起,利用捆绑法;
(3)甲、乙、丙三人两两不相邻,利用插空法;
(4)甲不排头,乙不排当中,利用间接法.
(2)甲、乙、丙三人必须在一起,利用捆绑法;
(3)甲、乙、丙三人两两不相邻,利用插空法;
(4)甲不排头,乙不排当中,利用间接法.
解答:
解:(1)甲固定不动,其余有
=720,即共有
=720种; …(3分)
(2)先排甲、乙、丙三人,有
,再把该三人当成一个整体,再加上另四人,相当于5人的全排列,即
,则共有
=720种; …(6分)
(3)先排甲、乙、丙之外的四人,有
,四人形成五个空位,甲、乙、丙三人排
这五个空位,有
,则共有
=1440种; …(10分)
(4)不考虑限制条件有
,而甲排头有
,乙排当中有
,这样重复了甲排头,乙排当中
一次,即
-2
+
=3720…(14分)
| A | 6 6 |
| A | 6 6 |
(2)先排甲、乙、丙三人,有
| A | 3 3 |
| A | 5 5 |
| A | 5 5 |
| A | 3 3 |
(3)先排甲、乙、丙之外的四人,有
| A | 4 4 |
这五个空位,有
| A | 3 5 |
| A | 3 5 |
| A | 4 4 |
(4)不考虑限制条件有
| A | 7 7 |
| A | 6 6 |
| A | 6 6 |
| A | 5 5 |
| A | 7 7 |
| A | 6 6 |
| A | 5 5 |
点评:本题考查计数原理的应用,考查学生的计算能力,正确运用解题方法是关键.

练习册系列答案
相关题目
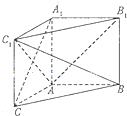 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,且AB=AC=AA1=1.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,且AB=AC=AA1=1.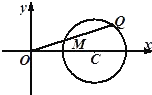 (理科)如图,圆C:(x-2)2+y2=1,点Q是圆C上任意一点,M是线段OQ的中点.
(理科)如图,圆C:(x-2)2+y2=1,点Q是圆C上任意一点,M是线段OQ的中点.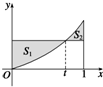 在区间[0,1]上给定曲线y=x2,试在此区间内确定点t的值,使图中阴影部分的面积:
在区间[0,1]上给定曲线y=x2,试在此区间内确定点t的值,使图中阴影部分的面积: