题目内容
如图,有一块半椭圆形钢板,其半轴长为2,短半轴长为1,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.
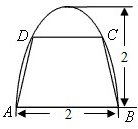
(Ⅰ)求面积S以x为自变量的函数式,并写出其定义域;
(Ⅱ)记f(x)=S2,求f(x)的最大值及面积S的最大值.

(Ⅰ)求面积S以x为自变量的函数式,并写出其定义域;
(Ⅱ)记f(x)=S2,求f(x)的最大值及面积S的最大值.
考点:函数解析式的求解及常用方法,椭圆的应用
专题:函数的性质及应用
分析:(Ⅰ)建立直角坐标系,设点C的横坐标为x.可得纵坐标y=2
(0<x<1),可表示出面积;(Ⅱ)由题意f(x)=S2=4(x+1)2(1-x2),0<x<1,求导数可得函数的极值,进而可得最值,可得答案.
| 1-x2 |
解答:
解:(Ⅰ)由题意,以AB的中点O为原点,
以AB所在直线为x轴,AB的垂直平分线为y轴,建立直角坐标系,
设点C的横坐标为x.点C的纵坐标y满足方程x2+
=1(y≥0),
解得y=2
(0<x<1),
∴S=
(2x+2)•2
=2(x+1)•
,其定义域为{x|0<x<1};
(Ⅱ)由题意f(x)=S2=4(x+1)2(1-x2),0<x<1,
∴f'(x)=8(x+1)2(1-2x).
令f'(x)=0,得x=
.
∵当0<x<
时,f'(x)>0;当
<x<1时,f'(x)<0,
∴f(
)是f(x)的极大值,也是最大值,
∴当x=
时,S也取得最大值,且最大值为
=
∴梯形面积S的最大值为
以AB所在直线为x轴,AB的垂直平分线为y轴,建立直角坐标系,
设点C的横坐标为x.点C的纵坐标y满足方程x2+
| y2 |
| 4 |
解得y=2
| 1-x2 |
∴S=
| 1 |
| 2 |
| 1-x2 |
| 1-x2 |
(Ⅱ)由题意f(x)=S2=4(x+1)2(1-x2),0<x<1,
∴f'(x)=8(x+1)2(1-2x).
令f'(x)=0,得x=
| 1 |
| 2 |
∵当0<x<
| 1 |
| 2 |
| 1 |
| 2 |
∴f(
| 1 |
| 2 |
∴当x=
| 1 |
| 2 |
f(
|
3
| ||
| 2 |
∴梯形面积S的最大值为
3
| ||
| 2 |
点评:本题考查函数解析式的求解,涉及导数和椭圆的方程,属中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
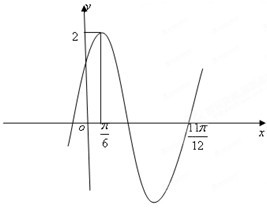 已知函数f(x)=Asin(wx+φ)(A>0,W>0,|φ|<
已知函数f(x)=Asin(wx+φ)(A>0,W>0,|φ|<