题目内容
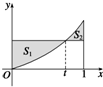 在区间[0,1]上给定曲线y=x2,试在此区间内确定点t的值,使图中阴影部分的面积:
在区间[0,1]上给定曲线y=x2,试在此区间内确定点t的值,使图中阴影部分的面积:(1)S1=S2;
(2)S=S1+S2最小.
考点:定积分在求面积中的应用
专题:综合题,导数的综合应用
分析:(1)利用定积分求出面积,根据S1=S2,建立方程,即可确定点t的值;
(2)S=S1+S2=
t3-t2+
(0≤t≤1),求导数,确定函数的单调性,即可求出最小值.
(2)S=S1+S2=
| 4 |
| 3 |
| 1 |
| 3 |
解答:
解:(1)∵S1=t•t2-∫
x2dx=
t3,
S2=∫
x2dx-(1-t)•t2=
t3-t2+
,
∵S1=S2,
∴
t3=
t3-t2+
,
∴t=
.
(2)∵S=S1+S2=
t3-t2+
(0≤t≤1),
S′=4t2-2t=4t(t-
),令S′=0,得t=0,t=
.
∵函数在(0,
)上S′<0,在(
,1)上S′>0,
∴t=
是极小值点,
又S(
)=
,S(0)=
,S(1)=
,
故t=
时,S=S1+S2最小.
t 0 |
| 2 |
| 3 |
S2=∫
1 t |
| 2 |
| 3 |
| 1 |
| 3 |
∵S1=S2,
∴
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
∴t=
| ||
| 3 |
(2)∵S=S1+S2=
| 4 |
| 3 |
| 1 |
| 3 |
S′=4t2-2t=4t(t-
| 1 |
| 2 |
| 1 |
| 2 |
∵函数在(0,
| 1 |
| 2 |
| 1 |
| 2 |
∴t=
| 1 |
| 2 |
又S(
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 2 |
| 3 |
故t=
| 1 |
| 2 |
点评:本题考查利用定积分求面积,解题的关键是确定被积区间及被积函数.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
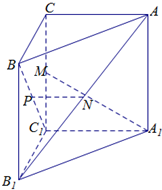 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=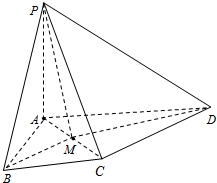 如图所示,PA⊥平面ABCD,△ABC为等边三角形,AP=AB,AC⊥CD,M为AC的中点.
如图所示,PA⊥平面ABCD,△ABC为等边三角形,AP=AB,AC⊥CD,M为AC的中点.