题目内容
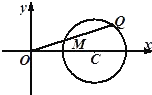 (理科)如图,圆C:(x-2)2+y2=1,点Q是圆C上任意一点,M是线段OQ的中点.
(理科)如图,圆C:(x-2)2+y2=1,点Q是圆C上任意一点,M是线段OQ的中点.(1)试求点M的轨迹方程.
(2)求轨迹所围成的图形的面积.
考点:轨迹方程
专题:计算题,直线与圆
分析:(1)取OC的中点P,由题意得到PM∥CQ,且PM∥CQ,|PM|=
|CQ|,故|PM|=
,可得M点的轨迹,从而得到圆的标准方程;
(2)利用圆的面积公式可得结论.
| 1 |
| 2 |
| 1 |
| 2 |
(2)利用圆的面积公式可得结论.
解答:
解:(1)设M(x,y),取OC的中点P,则点P的坐标为(1,0),连接PM,CQ,则
PM∥CQ,|PM|=
|CQ|,故|PM|=
,
∴M点的轨迹是以点P为圆心,
为半径的圆,
∴M点的轨迹方程是(x-1)2+y2=
;
(2)轨迹所围成的图形的面积S=
π.
PM∥CQ,|PM|=
| 1 |
| 2 |
| 1 |
| 2 |
∴M点的轨迹是以点P为圆心,
| 1 |
| 2 |
∴M点的轨迹方程是(x-1)2+y2=
| 1 |
| 4 |
(2)轨迹所围成的图形的面积S=
| 1 |
| 4 |
点评:本题考查圆的定义和标准方程,三角形的中位线的性质,得到PM∥CQ,|PM|=
|CQ|,是解题的关键.
| 1 |
| 2 |

练习册系列答案
相关题目
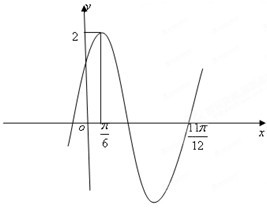 已知函数f(x)=Asin(wx+φ)(A>0,W>0,|φ|<
已知函数f(x)=Asin(wx+φ)(A>0,W>0,|φ|<