题目内容
已知集合A={x2-5x-14≤0}，B={x|m+1＜x＜2m-1}，若A∪B=A，求实数m的取值范围．
考点：并集及其运算
专题：集合
分析：求出A中不等式的解集确定出A，根据A与B的并集为A，分B为空集及不为空集两种情况，分别列出关于m的不等式，求出不等式的解集即可确定出m的范围．
解答：
解：由A中的不等式变形得：（x+2）（x-7）≤0，
解得：-2≤x≤7，即A=[-2，7]；
∵B=（m+1，2m-1），且A∪B=A，
∴当B=∅时，m+1≥2m-1，解得：m≤2，
当B≠∅时，
，
解得：-3≤m≤4；
则实数m的取值范围为（-∞，4]．
解得：-2≤x≤7，即A=[-2，7]；
∵B=（m+1，2m-1），且A∪B=A，
∴当B=∅时，m+1≥2m-1，解得：m≤2，
当B≠∅时，
|
解得：-3≤m≤4；
则实数m的取值范围为（-∞，4]．
点评：此题考查了并集及其运算，熟练掌握并集的定义是解本题的关键．
练习册系列答案
相关题目
小明家订了一份报纸，寒假期间他收集了每天报纸送达时间的数据，并绘制成频率分布直方图，如图所示．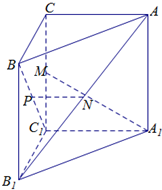
如图，已知三棱柱ABC-A1B1C1的侧棱与底面垂直，且∠ACB=90°，∠BAC=30°，BC=1，AA1=
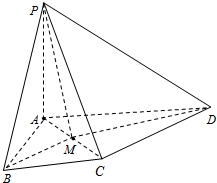如图所示，PA⊥平面ABCD，△ABC为等边三角形，AP=AB，AC⊥CD，M为AC的中点．