题目内容
2.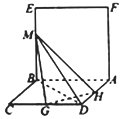 如图,已知平面ABEF⊥平面ABCD,四边形ABEF是正方形,四边形ABCD是菱形,且BC=2,∠BAD=60°,点G,H分别为边CD,DA的中点,点M是线段BE上的动点.
如图,已知平面ABEF⊥平面ABCD,四边形ABEF是正方形,四边形ABCD是菱形,且BC=2,∠BAD=60°,点G,H分别为边CD,DA的中点,点M是线段BE上的动点.(Ⅰ)求证:GH⊥平面BDM
(Ⅱ)求三棱锥D-MGH的体积的最大值.
分析 (Ⅰ)连接AC交BD于点O.则BE⊥AB.再由已知结合面面垂直的性质可得BE⊥平面ABCD,进一步得到BE⊥AC.由四边形ABCD为菱形,得BD⊥AC.由面面垂直的判定可得AC⊥平面BDM.由三角形中位线定理得GH∥AC,则GH⊥平面BDM;
(Ⅱ)在菱形ABCD中,利用正弦定理求得三角形DGM的面积,由图可得当点M与点E重合时,BM取最大值2,代入三棱锥体积公式求得三棱锥D-MGH的体积的最大值.
解答 (Ⅰ)证明:连接AC交BD于点O.
∵四边形ABEF为正方形.∴BE⊥AB.
又∵平面ABEF⊥平面ABCD,平面ABEF∩平面ABCD=AB.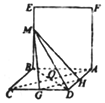
∴BE⊥平面ABCD.
又AC?平面ABCD,∴BE⊥AC.
∵四边形ABCD为菱形,∴BD⊥AC.
∵BD∩BE=B,∴AC⊥平面BDE,即AC⊥平面BDM.
∵G、H分别为DC、AD的中点,∴GH∥AC,
∴GH⊥平面BDM;
(Ⅱ)解:在菱形ABCD中,
由∠BAD=60°,得∠ADC=120°.
又∵DG=DH=1,∴${S}_{△DGM}=\frac{1}{2}DG•DH•sin120°=\frac{1}{2}×1×1×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{4}$.
∵BE⊥平面ABCD,即BM⊥平面ABCD,
∴${V}_{D-MGH}={V}_{M-DGH}=\frac{1}{3}{S}_{△DGH}•BM=\frac{\sqrt{3}}{12}BM$.
显然,当点M与点E重合时,BM取最大值2,
此时$({V}_{D-MGH})_{MAX}=\frac{\sqrt{3}}{12}×2=\frac{\sqrt{3}}{6}$,
即三棱锥D-MGH的体积的最大值为$\frac{\sqrt{3}}{6}$.
点评 本题考查直线与平面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案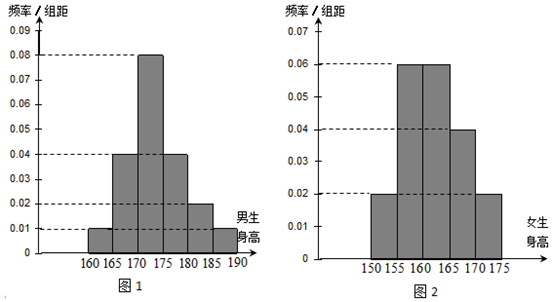
(1)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分比)的把握认为“身高与性别有关”?
| ≥170cm | <170cm | 总计 | |
| 男生身高 | |||
| 女生身高 | |||
| 总计 |
参考公式及参考数据如下:${k^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| P(K2≥k0) | 0.025 | 0.610 | 0.005 | 0.001 |
| k0 | 5.024 | 4.635 | 7.879 | 10.828 |
| A. | 1007 | B. | 1008 | C. | 1009 | D. | 1010 |
 已知一个几何体的三视图如图所示,则该几何体的体积为( )
已知一个几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{4}{3}$ | B. | 8 | C. | 4 | D. | $\frac{8}{3}$ |
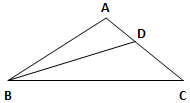 在△ABC中,内角A,B,C所对的边分别为a,b,c且2a cosC-c=2b.
在△ABC中,内角A,B,C所对的边分别为a,b,c且2a cosC-c=2b.