题目内容
10.设等差数列{an}的前n项和为Sn,且S2015>0,S2016<0.则数列{$\frac{{S}_{n}}{{a}_{n}}$}的最大的项的n的值为( )| A. | 1007 | B. | 1008 | C. | 1009 | D. | 1010 |
分析 等差数列{an}的前n项和为Sn,且S2015>0,S2016<0.可得S2015=2015a1008>0,S2016=1008(a1008+a1009)<0.可得a1008>0,a1009<0,公差d<0.可知:S1008最大,而a1008是正值中的最小值.即可得出.
解答 解:等差数列{an}的前n项和为Sn,且S2015>0,S2016<0.
∴S2015=$\frac{2015({a}_{1}+{a}_{2015})}{2}$=2015a1008>0,S2016=$\frac{2016({a}_{1}+{a}_{2016})}{2}$=1008(a1008+a1009)<0.
∴a1008>0,a1009<0,公差d<0.
可知:S1008最大,而a1008是正值中的最小值.
则数列{$\frac{{S}_{n}}{{a}_{n}}$}的最大的项的n的值是1008.
故选:B.
点评 本题考查了等差数列的性质及其通项公式求和公式及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.方程x2+(4+i)x+4+ai=0(a∈R)有实根b,且z=a+bi,则z=( )
| A. | 2-2i | B. | 2+2i | C. | -2+2i | D. | -2-2i |
5.已知等差数列{an}中,a3=4,a5=8,则a11=( )
| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
20.设△ABC的内角A,B,C的对边分别为a,b,c,若a=b,acosC=c(2-cosA),则cosB=( )
| A. | $\frac{{\sqrt{15}}}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
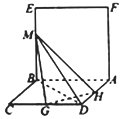 如图,已知平面ABEF⊥平面ABCD,四边形ABEF是正方形,四边形ABCD是菱形,且BC=2,∠BAD=60°,点G,H分别为边CD,DA的中点,点M是线段BE上的动点.
如图,已知平面ABEF⊥平面ABCD,四边形ABEF是正方形,四边形ABCD是菱形,且BC=2,∠BAD=60°,点G,H分别为边CD,DA的中点,点M是线段BE上的动点.