题目内容
11.已知圆C:x2+y2+2x-4y+3=0.(Ⅰ)设不过原点的直线l与圆C相切,且在x轴、y轴上的截距相等,求直线l的方程;
(Ⅱ)从圆C外一点P(x,y)向圆C引一条切线,切点为M,O为坐标原点,|MP|=|OP|,求点P的轨迹方程.
分析 ( I)通过切线在两坐标轴上的截距相等且不为零,设直线方程x+y=a,求出圆的圆心与半径,利用相切关系列出方程求解即可.
( II)利用已知条件,切线PM与半径CM垂直,通过PM|2=|PC|2-|CM|2=|OP|2,求解点P的轨迹方程为2x-4y+3=0.
解答 解:( I)∵切线在两坐标轴上的截距相等且不为零,
设直线方程x+y=a,
∵由圆C:x2+y2+2x-4y+3=0,得:(x+1)2+(y-2)2=2,
∴圆心坐标C(-1,2),半径r=$\sqrt{2}$,
∴圆心C(-1,2)到切线的距离等于圆半径$\sqrt{2}$,
即:$\frac{|-1+2-a|}{\sqrt{2}}$
∴a=-1或a=3,
所求切线方程为:x+y+1=0或x+y-3=0;
( II)设点P(x,y),
∵切线PM与半径CM垂直,
∴|PM|2=|PC|2-|CM|2=|OP|2
∴(x+1)2+(y-2)2-2=x2+y2
所以点P的轨迹方程为2x-4y+3=0.
点评 本题考查直线与圆的位置关系的应用,轨迹方程的求法,考查计算能力.

练习册系列答案
相关题目
1.方程x2+(4+i)x+4+ai=0(a∈R)有实根b,且z=a+bi,则z=( )
| A. | 2-2i | B. | 2+2i | C. | -2+2i | D. | -2-2i |
6.若$|{\overrightarrow a}|=\sqrt{2},|{\overrightarrow b}|=2$,且$({\overrightarrow a-\overrightarrow b})⊥\overrightarrow a$,则$\overrightarrow a$与$\overrightarrow b$的夹角是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
16.将函数$y=sin(x-\frac{π}{3})$的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再向右平移$\frac{π}{3}$个单位,所得图象的解析式是( )
| A. | y=sin2x | B. | $y=sin(\frac{x}{2}-\frac{π}{6})$ | C. | $y=-cos\frac{x}{2}$ | D. | $y=sin(2x-\frac{π}{6})$ |
3.已知圆C:(x-6)2+(y-8)2=1和两点A(-m,0),B(m,0)(m>0),若对圆上任意一点P,都有∠APB<90°,则m的取值范围是( )
| A. | (9,10) | B. | (1,9) | C. | (0,9) | D. | (9,11) |
20.设△ABC的内角A,B,C的对边分别为a,b,c,若a=b,acosC=c(2-cosA),则cosB=( )
| A. | $\frac{{\sqrt{15}}}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
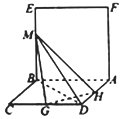 如图,已知平面ABEF⊥平面ABCD,四边形ABEF是正方形,四边形ABCD是菱形,且BC=2,∠BAD=60°,点G,H分别为边CD,DA的中点,点M是线段BE上的动点.
如图,已知平面ABEF⊥平面ABCD,四边形ABEF是正方形,四边形ABCD是菱形,且BC=2,∠BAD=60°,点G,H分别为边CD,DA的中点,点M是线段BE上的动点.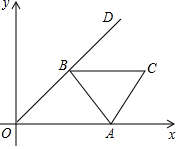 如图,边长为3的等边三角形ABC的顶点A在x轴的正半轴上移动,∠AOD=30°,顶点B在射线,OD上随之移动,则线段CO的最大值为3$\sqrt{3}$+3.
如图,边长为3的等边三角形ABC的顶点A在x轴的正半轴上移动,∠AOD=30°,顶点B在射线,OD上随之移动,则线段CO的最大值为3$\sqrt{3}$+3.