题目内容
12. 已知一个几何体的三视图如图所示,则该几何体的体积为( )
已知一个几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{4}{3}$ | B. | 8 | C. | 4 | D. | $\frac{8}{3}$ |
分析 几何体为四棱锥,俯视图为底面,主视图的高为棱锥的高,代入体积公式计算.
解答 解:由三视图可知几何体为底面为正方形的四棱锥,底面为边长为2的正方形,棱锥的高为2,
∴V=$\frac{1}{3}×{2}^{2}×2$=$\frac{8}{3}$.
故选:D.
点评 本题考查了空间几何体的三视图,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
3.已知圆C:(x-6)2+(y-8)2=1和两点A(-m,0),B(m,0)(m>0),若对圆上任意一点P,都有∠APB<90°,则m的取值范围是( )
| A. | (9,10) | B. | (1,9) | C. | (0,9) | D. | (9,11) |
20.设△ABC的内角A,B,C的对边分别为a,b,c,若a=b,acosC=c(2-cosA),则cosB=( )
| A. | $\frac{{\sqrt{15}}}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
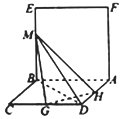 如图,已知平面ABEF⊥平面ABCD,四边形ABEF是正方形,四边形ABCD是菱形,且BC=2,∠BAD=60°,点G,H分别为边CD,DA的中点,点M是线段BE上的动点.
如图,已知平面ABEF⊥平面ABCD,四边形ABEF是正方形,四边形ABCD是菱形,且BC=2,∠BAD=60°,点G,H分别为边CD,DA的中点,点M是线段BE上的动点.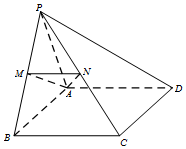 在四棱锥P-ABCD中,△PAB为正三角形,四边形ABCD为矩形,平面PAB⊥平面ABCD,AB=2AD,M、N分别为PB、PC的中点.
在四棱锥P-ABCD中,△PAB为正三角形,四边形ABCD为矩形,平面PAB⊥平面ABCD,AB=2AD,M、N分别为PB、PC的中点.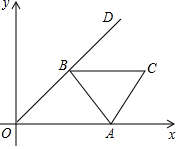 如图,边长为3的等边三角形ABC的顶点A在x轴的正半轴上移动,∠AOD=30°,顶点B在射线,OD上随之移动,则线段CO的最大值为3$\sqrt{3}$+3.
如图,边长为3的等边三角形ABC的顶点A在x轴的正半轴上移动,∠AOD=30°,顶点B在射线,OD上随之移动,则线段CO的最大值为3$\sqrt{3}$+3.