题目内容
设f(x)=1-(x-a)(x-b)(a<b),m,n为y=f(x)的两个零点,且m<n,则a,b,m,n的大小关系是( )
| A、a<m<n<b |
| B、m<a<b<n |
| C、a<b<m<n |
| D、m<n<a<b |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:构造函数f(x)=-(x-a)(x-b)(a<b),运用图象f(a)=f(b)=1,f(m)=f(n)=0,判断其意义,即可得出答案.
解答:
解:∵设f(x)=1-(x-a)(x-b)(a<b),m,n为y=f(x)的两个零点,
∴f(a)=f(b)=1,f(m)=f(n)=0,
根据二次函数的图象性质,y=1,y=0,两条直线与抛物线的交点可判断
a+b=m+n,(a<b,m<n)
∴m<a<b<n
故选:B
∴f(a)=f(b)=1,f(m)=f(n)=0,
根据二次函数的图象性质,y=1,y=0,两条直线与抛物线的交点可判断
a+b=m+n,(a<b,m<n)
∴m<a<b<n
故选:B

点评:本题考查了函数的性质与图象的应用,属于中档题.

练习册系列答案
相关题目
在钝角三角形ABC中,a=1,b=2,则最大边c的取值范围是( )
A、(
| ||
B、(
| ||
| C、(2,3) | ||
D、(
|
设A={x||x-a|<1},B={x|(x-1)(5-x)>0},若A∩B=∅,则实数a的取值范围是( )
| A、{a|0≤a≤6} |
| B、{a|a≤2或a≥4} |
| C、{a|a≤0或a≥6} |
| D、{a|2≤a≤4} |
已知命题p:对任意x∈R,总有x2≥0; q:x=2是方程x+3=0的根,则下列命题为真命题的是( )
| A、¬p∧q | B、p∧¬q |
| C、¬p∧¬q | D、p∧q |
如图是求
+
+
+…+
的值的程序框图,则判断框①中应填( )
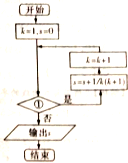
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 99×100 |

| A、k≤99? |
| B、k<99? |
| C、k≤100? |
| D、k<98? |
如果圆(x-a)2+(y-a)2=8上总存在到原点的距离为
的点,则实数a的取值范围是( )
| 2 |
| A、(-3,-1)∪(1,3) |
| B、(-3,3) |
| C、[-1,1] |
| D、[-3,-1]∪[1,3] |