题目内容
设A={x||x-a|<1},B={x|(x-1)(5-x)>0},若A∩B=∅,则实数a的取值范围是( )
| A、{a|0≤a≤6} |
| B、{a|a≤2或a≥4} |
| C、{a|a≤0或a≥6} |
| D、{a|2≤a≤4} |
考点:交集及其运算
专题:集合
分析:由已知得a+1≤1或a-1≥5,由此能求出实数a的取值范围.
解答:
解:∵A={x||x-a|<1}={x|a-1<x<a+1},
B={x|(x-1)(5-x)>0}={x|1<x<5},
又A∩B=∅,
∴a+1≤1或a-1≥5,
解得a≤0或a≥6.
故选:C.
B={x|(x-1)(5-x)>0}={x|1<x<5},
又A∩B=∅,
∴a+1≤1或a-1≥5,
解得a≤0或a≥6.
故选:C.
点评:本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意不等式性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(理做)已知函数f(x)=
-lnx,函数y=f(|x|)的零点个数为n,则n=( )
| 1 |
| x-1 |
| A、2 | B、4 | C、6 | D、8 |
下列式子正确的是( )
A、
| ||||||||||||
B、
| ||||||||||||
C、λ(μa)=(λμ)
| ||||||||||||
D、
|
已知:p:x≥k,q:
<0,如果p是q的充分不必要条件,则k的取值范围是( )
| 2-x |
| x+1 |
| A、[2,+∞) |
| B、(2,+∞) |
| C、[1,+∞) |
| D、(-∞,-1] |
设a∈R,若函数y=ex+ax,x∈R,有大于-1的极值点,则( )
| A、a<-1 | ||
| B、a>-1 | ||
C、a<-
| ||
D、a>-
|
设f(x)=1-(x-a)(x-b)(a<b),m,n为y=f(x)的两个零点,且m<n,则a,b,m,n的大小关系是( )
| A、a<m<n<b |
| B、m<a<b<n |
| C、a<b<m<n |
| D、m<n<a<b |
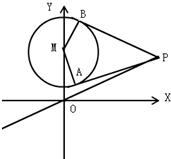 如图,已知圆M:x2+(y-4)2=4,直线l的方程为x-2y=0,点P是直线l上一动点,过点P作圆的切线PA、PB,切点为A、B.
如图,已知圆M:x2+(y-4)2=4,直线l的方程为x-2y=0,点P是直线l上一动点,过点P作圆的切线PA、PB,切点为A、B.