题目内容
如图，正六边形ABCDEF的边长为
，则
•
=
| 3 |
| AC |
| DB |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：
•
=(
+
)•(
+
)，根据正六边形的内角为120°，及正六边形的对称性可求得向量
，
的夹角，又已知正六边形的边长为
，所以进行数量积的运算即可求得答案．
| AC |
| DB |
| AB |
| BC |
| DC |
| CB |
| AB |
| DC |
| 3 |
解答：
解：如图，连接AD，延长AB，DC相交于M点，则△ADM为等边三角形；
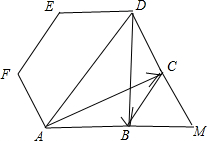根据正六边形的内角为120°；
∴
•
=(
+
)•(
+
)=
•
+
•
+
•
+
•
=
•
cos60°+
•
cos120°+
•
cos120°-
•
=-
．
故答案为：-
．
根据正六边形的内角为120°；∴
| AC |
| DB |
| AB |
| BC |
| DC |
| CB |
| AB |
| DC |
| AB |
| CB |
| BC |
| DC |
| BC |
| CB |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 9 |
| 2 |
故答案为：-
| 9 |
| 2 |
点评：考查对正六边形的认识，向量的加法运算，向量的夹角，以及向量数量积的计算公式．
练习册系列答案
相关题目
设F1、F2是双曲线
-
=1（a＞0，b＞0）的左、右焦点，A是其右支上一点，连接AF1交双曲线的左支于点B，若|AB|=|AF2|，且∠BAF2=60°，则该双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
△ABC的外接圆半径为R，∠C=60°，则
的取值范围是（ ）
| a+b |
| R |
A、[
| ||||
B、[
| ||||
C、（
| ||||
D、（
|
已知点A（1，-2，0）和向量
=（-3，4，12），
∥
且|
|=2|
|，则B点坐标为（ ）
| a |
| AB |
| a |
| AB |
| a |
| A、（-5，6，24）或（7，-10，-24） |
| B、（5，-6，24，）或（7，-10，-24） |
| C、（5，6，24）或（7，-10，-24） |
| D、（-5，6，24）或（7，10，-24） |