题目内容
推导等差数列的前n项和公式
等差数列：Sn=
．
等差数列：Sn=
| n(a1+an) |
| 2 |
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：可得Sn=a1+a2+a3+…+an，Sn=an+an-1+an-2+…+a1，两式相加结合等差数列的性质可得．
解答：
证明：∵Sn=a1+a2+a3+…+an，
还可得Sn=an+an-1+an-2+…+a1，
两式相加可得2Sn=（a1+an）+（a2+an-1）+…+（an+a1），
由等差数列的性质可得a1+an=a2+an-1=…=（an+a1），
∴2Sn=n（a1+an），∴Sn=
．
还可得Sn=an+an-1+an-2+…+a1，
两式相加可得2Sn=（a1+an）+（a2+an-1）+…+（an+a1），
由等差数列的性质可得a1+an=a2+an-1=…=（an+a1），
∴2Sn=n（a1+an），∴Sn=
| n(a1+an) |
| 2 |
点评：本题考查等差数列的求和公式，倒序相加是解决问题的关键，属基础题．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
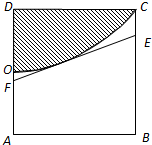如图，有一边长为2米的正方形钢板ABCD缺损一角（图中的阴影部分），边缘线OC是以直线AD为对称轴，以线段AD的中点O为顶点的抛物线的一部分．工人师傅要将缺损一角切割下来，使剩余的部分成为一个直角梯形．把-495°表示成K•360°+θ（k∈Z）的形式，其中使|θ|最小的θ值是（ ）
| A、-135° | B、-45° |
| C、45° | D、135° |
三个数e-
，log0.23，lnπ的大小关系为（ ）
| 2 |
A、log0.23＜e-
| ||
B、log0.23＜lnπ＜e-
| ||
C、e-
| ||
D、log0.23＜lnπ＜e-
|