题目内容
把-495°表示成K•360°+θ（k∈Z）的形式，其中使|θ|最小的θ值是（ ）
| A、-135° | B、-45° |
| C、45° | D、135° |
考点：终边相同的角
专题：计算题,三角函数的求值
分析：利用-495°=-135°-360°，它的终边与-135°的终边相同，故使|θ|最小的θ 为-135°
解答：
解：-495°=-135°-360°，它的终边与-135°的终边相同，在第三象限内，
故选：A．
故选：A．
点评：本题考查终边相同的角的表示方法，考查基本概念，基本知识的熟练程度，是基础题．
练习册系列答案
相关题目
若m+n=1（mn＞0），则
+
的最小值为（ ）
| 1 |
| m |
| 1 |
| n |
| A、1 | B、2 | C、3 | D、4 |
等差数列{an}满足a8＞0，a9＜0，则n=（ ）时，{an}前n项和最大．
| A、6 | B、7 | C、8 | D、9 |
已知数列{an}的前n项和Sn=an-1（a是不为0的常数），那么数列{an}（ ）
| A、一定是等差数列 |
| B、一定是等比数列 |
| C、或者是等差数列或者是等比数列 |
| D、既不是等差数列也不是等比数列 |
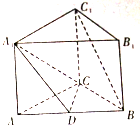如图，直三棱柱ABC-A