题目内容
已知O为坐标原点，点A（2，0），B（0，2），C（cosα，sinα），且0＜α＜π．
（Ⅰ）若
•
=
，求tanα的值；
（Ⅱ）若|
+
|=
，求
与
的夹角．
（Ⅰ）若
| AC |
| BC |
| 7 |
| 5 |
（Ⅱ）若|
| OA |
| OC |
| 7 |
| OB |
| OC |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（Ⅰ）由题设条件求出
，
，再由
•
=
，利用已知条件得到三角函数的表达式，利用三角函数的性质能求出tanα．
（Ⅱ）由已知条件，先求出
，
，
，由|
+
|=
，两边平方结合题设条件能求出α=
，由此能求出
与
的夹角．
| AC |
| BC |
| AC |
| BC |
| 7 |
| 5 |
（Ⅱ）由已知条件，先求出
| OA |
| OB |
| OC |
| OA |
| OC |
| 7 |
| π |
| 3 |
| OB |
| OC |
解答：
解：（Ⅰ）∵O为坐标原点，点A（2，0），B（0，2），C（cosα，sinα），
∴
=(cosα-2，sinα)，
=(cosα，sinα-2)，
∵
•
=
，
∴cosα（cosα-2）+sinα（sinα-2）=
，
∴sinα+cosα=-
，①
两边同时平方，得1+2sinαcosα=
，
∴sinαcosα=-
，
∵0＜α＜π，∴cosα＜0，∴α∈(
，π)，
∴sinα-cosα=
=
=
，②
由①②，得sinα=
，cosα=-
，
∴tanα=-
．
（Ⅱ）∵|
+
|=
，
两边平方得到|
|2+|
|2+2
•
=7，
∵O为坐标原点，点A（2，0），B（0，2），C（cosα，sinα），
∴|
|2=4，|
|2=1，
∴
•
=1=2cosα，
∵0＜α＜π，α=
，
设求
与
的夹角为θ，
则cosθ=
=
=sin
=
，
∴θ=
．
∴
| AC |
| BC |
∵
| AC |
| BC |
| 7 |
| 5 |
∴cosα（cosα-2）+sinα（sinα-2）=
| 7 |
| 5 |
∴sinα+cosα=-
| 1 |
| 5 |
两边同时平方，得1+2sinαcosα=
| 1 |
| 25 |
∴sinαcosα=-
| 12 |
| 25 |
∵0＜α＜π，∴cosα＜0，∴α∈(
| π |
| 2 |
∴sinα-cosα=
| (sinα-cosα)2 |
1+
|
| 7 |
| 5 |
由①②，得sinα=
| 3 |
| 5 |
| 4 |
| 5 |
∴tanα=-
| 3 |
| 4 |
（Ⅱ）∵|
| OA |
| OC |
| 7 |
两边平方得到|
| OA |
| OC |
| OA |
| OC |
∵O为坐标原点，点A（2，0），B（0，2），C（cosα，sinα），
∴|
| OA |
| OC |
∴
| OA |
| OC |
∵0＜α＜π，α=
| π |
| 3 |
设求
| OB |
| OC |
则cosθ=
| ||||
|
|
| 2sinα |
| 2 |
| π |
| 3 |
| ||
| 2 |
∴θ=
| π |
| 6 |
点评：本题考查平面向量的坐标运算，考查三角函数的知识，是中档题，解题时要注意三角函数恒等式的合理运用．
练习册系列答案
相关题目
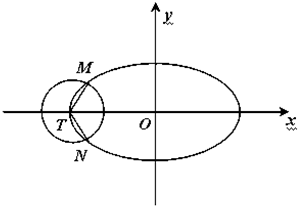如图，已知椭圆C：