题目内容
已知函数f(x)=-ax2+ax-1,x∈[0,1],若a≥
,则f(x)的最大值是 .
| 1 |
| 2 |
考点:二次函数的性质
专题:函数的性质及应用
分析:由二次函数的解析式及a的范围知抛物线开口向下,对称轴x=1,从而求出顶点坐标即为最大值.
解答:
解:由函数f(x)=-ax2+ax-1,a≥
,
∴抛物线开口向下,对称轴x=1,
∴顶点的纵坐标的值即为f(x)的最大值,
∴f(x)最大=
=
.
故答案为:
| 1 |
| 2 |
∴抛物线开口向下,对称轴x=1,
∴顶点的纵坐标的值即为f(x)的最大值,
∴f(x)最大=
| 4a-a2 |
| -4a |
| a-4 |
| 4 |
故答案为:
| a-4 |
| 4 |
点评:本题考察了二次函数的图象及性质问题,对称轴及顶点坐标,是一道基础题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
下列函数是偶函数,且在[0,1]上单调递增的是( )
A、y=cos(x+
| ||
| B、y=1-2cos22x | ||
| C、y=-x2 | ||
| D、y=|sin(π+x)| |
设f(x)=
,则
f(x)dx等于( )
|
| ∫ | 2 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
“a>1”是“函数y=x2-2ax+a有两个零点”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
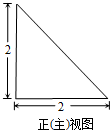 某三棱锥的三视图是三个全等的等腰直角三角形,且正(主)视图如图所示,则此三棱锥的表面积为( )
某三棱锥的三视图是三个全等的等腰直角三角形,且正(主)视图如图所示,则此三棱锥的表面积为( )A、6+2
| ||||
B、4+4
| ||||
C、6+4
| ||||
D、4+4
|