题目内容
已知数列{an},{bn}中,对任意n∈N*都有:a1b1+a2b2+a3b3+…+an-1bn-1+anbn=(n-1)•2n+1.
(1)若数列{an}是等差数列,数列{bn}是否为等比数列?若是,请求出通项公式,若不是,请说明理由;
(2)求证:
<
.
(1)若数列{an}是等差数列,数列{bn}是否为等比数列?若是,请求出通项公式,若不是,请说明理由;
(2)求证:
| n |
 |
| i=1 |
| 1 |
| a ibi |
| 3 |
| 2 |
考点:等差数列与等比数列的综合
专题:综合题,等差数列与等比数列
分析:(1)根据条件,再写一式,两式相减,写出等差数列的通项n=a1+(n-1)d,从而可得数列{bn}的通项,利用数列{bn}是等比数列,确定条件,从而可得结论;
(2)
=
+
+…+
,利用放缩法,结合等比数列的求和公式,即可证得结论.
(2)
| n |
 |
| i=1 |
| 1 |
| a ibi |
| 1 |
| 1×1 |
| 1 |
| 2×2 |
| 1 |
| n×2n-1 |
解答:
(1)解:依题意,由a1b1+a2b2+a3b3+…+an-1bn-1+anbn=(n-1)•2n+1,
可得a1b1+a2b2+a3b3+…+an-1bn-1=(n-2)•2n-1+1(n≥2),
两式相减可得anbn=n•2n-1,
设等差数列的首项为a1,公差为d,则an=a1+(n-1)d
∵anbn=n•2n-1,
∴bn=
(n≥2)
∴bn=
若数列{bn}是等比数列,则a1=d≠0
∴a1=d≠0时,数列{bn}是等比数列,bn=
;a1≠d时,数列{bn}不是等比数列;
(2)证明:由(1)知anbn=n•2n-1,n=1,2时,结论成立.
∴
=
+
+…+
<
+
+…+
(n≥3)
=1+
+
×
≤1+
+
=
.
可得a1b1+a2b2+a3b3+…+an-1bn-1=(n-2)•2n-1+1(n≥2),
两式相减可得anbn=n•2n-1,
设等差数列的首项为a1,公差为d,则an=a1+(n-1)d
∵anbn=n•2n-1,
∴bn=
| n•2n-1 |
| a1+(n-1)d |
∴bn=
| 2n-1 | ||
|
若数列{bn}是等比数列,则a1=d≠0
∴a1=d≠0时,数列{bn}是等比数列,bn=
| 2n-1 |
| d |
(2)证明:由(1)知anbn=n•2n-1,n=1,2时,结论成立.
∴
| n |
 |
| i=1 |
| 1 |
| a ibi |
| 1 |
| 1×1 |
| 1 |
| 2×2 |
| 1 |
| n×2n-1 |
| 1 |
| 1×1 |
| 1 |
| 2×2 |
| 1 |
| 2×2n-1 |
=1+
| 1 |
| 4 |
| 1 |
| 8 |
1-(
| ||
1-
|
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
点评:本题考查等差数列与等比数列的综合,考查不等式的证明,正确运用等差数列与等比数列的通项是关键.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 如图是一个几何体的三视图,其正视图和侧视图是两个全等的等腰梯形,上底边长为2,
如图是一个几何体的三视图,其正视图和侧视图是两个全等的等腰梯形,上底边长为2,下底边长为6,腰长为5,则该几何体的侧面积为( )
| A、10π | B、20π |
| C、30π | D、40π |
一颗正方体骰子,共六个面的点数分别是1、2、3、4、5、6,将这颗骰子连续掷三次观察向上的点数,则三次点数和为16的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
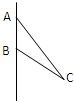 如图,在△ABC中,AB=3,BC=5,∠ABC=120°将△ABC绕直线AB旋转一周,则所形成的旋转体的侧面积是
如图,在△ABC中,AB=3,BC=5,∠ABC=120°将△ABC绕直线AB旋转一周,则所形成的旋转体的侧面积是