题目内容
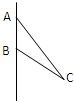如图，在△ABC中，AB=3，BC=5，∠ABC=120°将△ABC绕直线AB旋转一周，则所形成的旋转体的侧面积是考点：旋转体（圆柱、圆锥、圆台）
专题：计算题,空间位置关系与距离
分析：在△ABC中，由余弦定理，得AC=7，过点C作CO⊥AB，垂足为O，所形成的旋转体的表面积S为圆锥AO和圆锥BO的侧面积之和．
解答：
解：在△ABC中，
∵△ABC中，AB=3，BC=5，∠ABC=120°，
∴由余弦定理，得AC=7，
过点C作CO⊥AB，垂足为O，
则OC=BCsin60°=
，
由图知，所形成的旋转体的表面积S为圆锥AO和圆锥BO的侧面积之和．
∴S=π×OC×(BC+AC)=30
π．
故答案为：30
π．
解：在△ABC中，∵△ABC中，AB=3，BC=5，∠ABC=120°，
∴由余弦定理，得AC=7，
过点C作CO⊥AB，垂足为O，
则OC=BCsin60°=
5
| ||
| 2 |
由图知，所形成的旋转体的表面积S为圆锥AO和圆锥BO的侧面积之和．
∴S=π×OC×(BC+AC)=30
| 3 |
故答案为：30
| 3 |
点评：本题考查旋转体的侧面积的求法，解题时要认真审题，仔细解答，注意余弦定理的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
已知点P是△ABC所在平面内一点，则
+
+
=
是点P在线段AC上的（ ）
| PA |
| PB |
| PC |
| AB |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
某高校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩，按成绩共分成五组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]，得到的频率分布直方图如图所示，同时规定成绩在85分以上（含85分）的学生为“优秀”，成绩小于85分的学生为“良好”，且只有成绩为“优秀”的学生才能获得面试资格．某几何体的三视图如图所示，则该几何体的表面积为（ ）
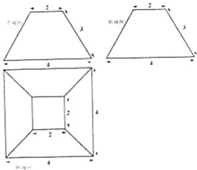
A、20+12
| ||
B、20+24
| ||
C、20+12
| ||
| D、56 |
