题目内容
已知数列{an}的各项均不为零,且前n项和为Sn,若对于任意的正整数m,n,恒有(n-m)Sn+m=(n+m)(Sn-Sm).
(1)求
的值;
(2)求证:数列{an}为等差数列;
(3)若ap,aq,ar,as成等比数列,且a1≠a2,求证:q-p,r-q,s-r成等比数列.
(1)求
| S3 |
| a2 |
(2)求证:数列{an}为等差数列;
(3)若ap,aq,ar,as成等比数列,且a1≠a2,求证:q-p,r-q,s-r成等比数列.
考点:等比关系的确定,等差数列的性质
专题:等差数列与等比数列
分析:(1)由对于任意的正整数m,n,恒有(n-m)Sn+m=(n+m)(Sn-Sm).令m=1,n=2,可得S3=3a2,进而得到答案;
(2)令m=1,则(n-1)Sn+1=(n+1)(Sn-S1),可得an+3-an+2=an+2-an+1,结合(1)中结论得到a2-a1=a3-a2也成立,则an+2-an+1=an+1-an,即数列{an}为等差数列;
(3)数列{an}的公差不为零且ap,aq,ar,as成等比数列,可得
=
=
,即q-p=r-q=s-r≠0,即q-p,r-q,s-r成等比数列,且公比不为1.
(2)令m=1,则(n-1)Sn+1=(n+1)(Sn-S1),可得an+3-an+2=an+2-an+1,结合(1)中结论得到a2-a1=a3-a2也成立,则an+2-an+1=an+1-an,即数列{an}为等差数列;
(3)数列{an}的公差不为零且ap,aq,ar,as成等比数列,可得
| aq |
| ap |
| ar |
| aq |
| as |
| ar |
解答:
(1)解:∵对于任意的正整数m,n,恒有(n-m)Sn+m=(n+m)(Sn-Sm).
令m=1,n=2,则S3=3a2,
∴
=3
(2)证明:令m=1,则(n-1)Sn+1=(n+1)(Sn-S1),
∴nSn+2=(n+2)(Sn+1-S1),
∴nSn+2-(n-1)Sn+1=(n+2)(Sn+1-S1)-(n+1)(Sn-S1),
∴nan+2=(n+1)an+1-S1,∴(n+1)an+3=(n+2)an+2-S1,
∴(n+1)an+3-nan+2=(n+2)an+2-(n+1)an+1,
∴an+3-an+2=an+2-an+1,又∵S3=2a2,
∴a2-a1=a3-a2,
∴an+2-an+1=an+1-an,
∴数列{an}为等差数列
(3)证明:∵a1≠a2,
∴数列{an}的公差不为零
∵ap,aq,ar,as成等比数列,
∴
=
=
记公比为x,则x≠1,且xq-p=xr-q=xs-r
∴q-p=r-q=s-r≠0
∴q-p,r-q,s-r成等比数列,且公比不为1.
令m=1,n=2,则S3=3a2,
∴
| S3 |
| a2 |
(2)证明:令m=1,则(n-1)Sn+1=(n+1)(Sn-S1),
∴nSn+2=(n+2)(Sn+1-S1),
∴nSn+2-(n-1)Sn+1=(n+2)(Sn+1-S1)-(n+1)(Sn-S1),
∴nan+2=(n+1)an+1-S1,∴(n+1)an+3=(n+2)an+2-S1,
∴(n+1)an+3-nan+2=(n+2)an+2-(n+1)an+1,
∴an+3-an+2=an+2-an+1,又∵S3=2a2,
∴a2-a1=a3-a2,
∴an+2-an+1=an+1-an,
∴数列{an}为等差数列
(3)证明:∵a1≠a2,
∴数列{an}的公差不为零
∵ap,aq,ar,as成等比数列,
∴
| aq |
| ap |
| ar |
| aq |
| as |
| ar |
记公比为x,则x≠1,且xq-p=xr-q=xs-r
∴q-p=r-q=s-r≠0
∴q-p,r-q,s-r成等比数列,且公比不为1.
点评:本题考查的知识点是等差数列的性质和定义,等比数列的性质和定义,是等差数列与等比数列的综合应用,难度中档.

练习册系列答案
相关题目
以下四个命题中错误的是( )
| A、已知随机变量X~N(2,9)P(X>c+1)=P(X<c+1),则c=1 | ||||
| B、两个随机变量相关性越强,则相关系数r的绝对值越接近于1 | ||||
C、在回归直线方程
| ||||
| D、对分类变量X与Y的随机变量K2的观测值k,k越小,“X与Y有关系”的把握程度越大 |
 在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,点M,N在棱CC1,BB1上,且CM=B1N,则四棱锥A-BCMN的体积为
在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,点M,N在棱CC1,BB1上,且CM=B1N,则四棱锥A-BCMN的体积为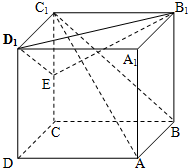 如图,已知长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连结BC1,过点B1作BC1的垂线交CC1于E.
如图,已知长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连结BC1,过点B1作BC1的垂线交CC1于E.