题目内容
在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,且tanC+3tanB=0.
(1)求∠A的最大值;
(2)若b2+2a=c2,求a的值.
(1)求∠A的最大值;
(2)若b2+2a=c2,求a的值.
考点:正弦定理
专题:解三角形
分析:(1)由已知化简可得tanA=
≤
,所以有A≤
,即A的最大值为
;
(2)由(1)可求得a+2bcosC=0,又由余弦定理可得2a2+b2-c2=0,结合已知即可求出a的值.
| -2tanC |
| tan2C+3 |
| ||
| 3 |
| π |
| 6 |
| π |
| 6 |
(2)由(1)可求得a+2bcosC=0,又由余弦定理可得2a2+b2-c2=0,结合已知即可求出a的值.
解答:
解:(1)tanC+3tanB=0
⇒sinBcosC+cosBsinC+2sinBcosC=0
⇒sin(B+C)+2sinBcosC=0
⇒sinA+2sinBcosC=0
⇒sinA+2(sinAcosC+cosAsinC)cosC=0
化简整理可得:tanA=
=
=
;
因为tanC<0,所以:tanA=
≤
,所以:A≤
,即A的最大值为
.
(2)b2+2a=c2…①
而又有(1)得sinA+2sinBcosC=0,
故由正弦定理可知a+2bcosC=0,又cosC=
,
所以得2a2+b2-c2=0…②
由①②联立可解得:a=1.
⇒sinBcosC+cosBsinC+2sinBcosC=0
⇒sin(B+C)+2sinBcosC=0
⇒sinA+2sinBcosC=0
⇒sinA+2(sinAcosC+cosAsinC)cosC=0
化简整理可得:tanA=
| -2sinCcosC |
| 1+2cos2C |
| -2sinCcosC |
| sin2C+3cos2C |
| -2tanC |
| tan2C+3 |
因为tanC<0,所以:tanA=
| -2 | ||
-(-tanC+
|
| ||
| 3 |
| π |
| 6 |
| π |
| 6 |
(2)b2+2a=c2…①
而又有(1)得sinA+2sinBcosC=0,
故由正弦定理可知a+2bcosC=0,又cosC=
| a2+b2-c2 |
| 2ab |
所以得2a2+b2-c2=0…②
由①②联立可解得:a=1.
点评:本题主要考察了正弦定理、余弦定理的综合应用,所以中档题.

练习册系列答案
相关题目
已知函数f(x)=
,点O为坐标原点,点An(n,f(n))(n∈N*).若记直线OAn的倾斜角为θn,则tanθ1+tanθ2+…+tanθn=( )
| 1 |
| x+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
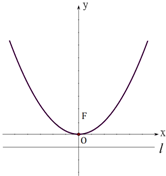 如图,抛物线C的顶点为坐标原点O,焦点F在y轴上,准线l与圆x2+y2=1相切.
如图,抛物线C的顶点为坐标原点O,焦点F在y轴上,准线l与圆x2+y2=1相切.