题目内容
在直角坐标平面内,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知点A、B的极坐标分别为(1 ,
)、(3 ,
),曲线C的参数方程为
(α为参数).
(Ⅰ)求直线AB的直角坐标方程;
(Ⅱ)若直线AB和曲线C只有一个交点,求r的值.
| π |
| 3 |
| 2π |
| 3 |
|
(Ⅰ)求直线AB的直角坐标方程;
(Ⅱ)若直线AB和曲线C只有一个交点,求r的值.
考点:简单曲线的极坐标方程
专题:计算题,直线与圆,坐标系和参数方程
分析:(Ⅰ)由x=ρcosθ,y=ρsinθ,可将A,B化为直角坐标,再由直线方程的形式,即可得到AB的方程;
(Ⅱ)运用同角的平方关系,可将曲线C化为普通方程即为圆,再由直线和圆相切:d=r,即可得到半径r.
(Ⅱ)运用同角的平方关系,可将曲线C化为普通方程即为圆,再由直线和圆相切:d=r,即可得到半径r.
解答:
解:(Ⅰ)∵点A、B的极坐标分别为(1 ,
)、(3 ,
),
∴点A、B的直角坐标分别为(
,
)、(-
,
),
∴直线AB的直角坐标方程为2
x+4y-3
=0;
(Ⅱ)由曲线C的参数方程
(α为参数),化为普通方程为x2+y2=r2,
∵直线AB和曲线C只有一个交点,
∴半径r=
=
.
| π |
| 3 |
| 2π |
| 3 |
∴点A、B的直角坐标分别为(
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
3
| ||
| 2 |
∴直线AB的直角坐标方程为2
| 3 |
| 3 |
(Ⅱ)由曲线C的参数方程
|
∵直线AB和曲线C只有一个交点,
∴半径r=
|3
| ||||
|
3
| ||
| 14 |
点评:本题考查极坐标和直角坐标的互化,以及极坐标方程和直角坐标方程的互化,考查直线和圆的位置关系,考查运算能力,属于基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,根据收集到的数据(如下表),由最小二乘法求得回归直线方程
=0.68
+54.6,利用下表中数据推断a的值为( )
| ? |
| y |
| ? |
| x |
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(min) | 62 | a | 75 | 81 | 89 |
| A、68.2 | B、68 |
| C、69 | D、67 |
如图,正方体ABCD-A1B1C1D1中,异面直线BC1和CD1所成角为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
一组数据中每个数据都减去50构成一组新数据,则这组新数据的平均数是1.2,方差是4.4,则原来一组数的方差为( )
| A、3.2 | B、4.4 |
| C、4.8 | D、5.6 |
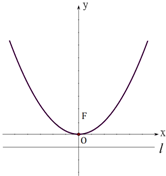 如图,抛物线C的顶点为坐标原点O,焦点F在y轴上,准线l与圆x2+y2=1相切.
如图,抛物线C的顶点为坐标原点O,焦点F在y轴上,准线l与圆x2+y2=1相切.