题目内容
以下四个命题中错误的是( )
| A、已知随机变量X~N(2,9)P(X>c+1)=P(X<c+1),则c=1 | ||||
| B、两个随机变量相关性越强,则相关系数r的绝对值越接近于1 | ||||
C、在回归直线方程
| ||||
| D、对分类变量X与Y的随机变量K2的观测值k,k越小,“X与Y有关系”的把握程度越大 |
考点:命题的真假判断与应用
专题:概率与统计
分析:根据正态曲线关于x=2对称,得到两个概率相等的区间关于x=2对称,得到关于c的方程,解方程即可判断A;
根据相关系数与相关性的关系,可判断B;
根据回归系数的意义,可判断C;
根据观测值与把握程序的关系,可判断D.
根据相关系数与相关性的关系,可判断B;
根据回归系数的意义,可判断C;
根据观测值与把握程序的关系,可判断D.
解答:
解:∵正态曲线关于x=2对称,且P(X>c+1)=P(X<c+1),∴c+1+c+1=2×2,解得c=1,故A正确;
两个随机变量相关性越强,则相关系数r的绝对值越接近于1,故B正确;
在回归直线方程
=0.2x+12中,当解释变量x每增加一个单位时,预报变量
平均增加0.2个单位,故C正确;
对分类变量X与Y的随机变量K2的观测值k,k越大,“X与Y有关系”的把握程度越大,故D错误;
故选:D
两个随机变量相关性越强,则相关系数r的绝对值越接近于1,故B正确;
在回归直线方程
| ∧ |
| y |
| ∧ |
| y |
对分类变量X与Y的随机变量K2的观测值k,k越大,“X与Y有关系”的把握程度越大,故D错误;
故选:D
点评:本题以命题的真假判断为载体,考查了正态分布,相关关系,独立性检验和回归分析等统计内容,难度不大,属于基础题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
已知三棱锥的底面是正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )
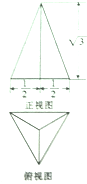

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)=
,点O为坐标原点,点An(n,f(n))(n∈N*).若记直线OAn的倾斜角为θn,则tanθ1+tanθ2+…+tanθn=( )
| 1 |
| x+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|