题目内容
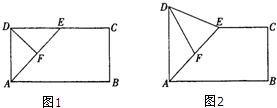 如图所示,在长方形ABCD中,AB=2BC,E为CD的中点,F为AE的中点,现在沿AE将△ADE向上折起.
如图所示,在长方形ABCD中,AB=2BC,E为CD的中点,F为AE的中点,现在沿AE将△ADE向上折起.(1)在线段AB上是否存在一点K,使BC∥平面DFK?若存在,请证明你的结论;若不存在,请说明理由.
(2)若平面ADE⊥平面ABCE,求证:AD⊥BE.
考点:平面与平面垂直的性质
专题:空间位置关系与距离
分析:(Ⅰ)线段AB上存在一点K,且当AK=
时,BC∥面DFK;设H为AB的中点,连接EH,则BC∥EH,利用三角形的中位线定理即可证明FK∥BC,再利用线面平行的判定定理即可证明;
(II)利用勾股定理的逆定理即可证明BE⊥AE,又面ADE⊥面ABCE,利用面面垂直的性质可得BE⊥平面ADE,再利用面面垂直的判定定理即可证明结论.
| 1 |
| 4 |
(II)利用勾股定理的逆定理即可证明BE⊥AE,又面ADE⊥面ABCE,利用面面垂直的性质可得BE⊥平面ADE,再利用面面垂直的判定定理即可证明结论.
解答:
解:(Ⅰ)线段AB上存在一点K,且当AK=
时,BC∥面DFK,

证明如下
设H为AB的中点,连接EH,则BC∥EH
又∵AK=
,F为AE的中点,
∴KF∥EH,∴KF∥BC,
∵KF?面DFK,BC?面DFK,
∴BC∥面DFK.
(II)∵在折起前的图形中E为CD的中点,AB=2,BC=1,
∴在折起后的图形中:AE=BE=
,
从而AE2+BE2=4=AB2
∴AE⊥BE.
∵面ADE⊥面ABCE,面ADE∩面ABCE=AE,
∴BE⊥平面ADE,∵AD?平面ADE
∴BE⊥AD
| 1 |
| 4 |

证明如下
设H为AB的中点,连接EH,则BC∥EH
又∵AK=
| 1 |
| 4 |
∴KF∥EH,∴KF∥BC,
∵KF?面DFK,BC?面DFK,
∴BC∥面DFK.
(II)∵在折起前的图形中E为CD的中点,AB=2,BC=1,
∴在折起后的图形中:AE=BE=
| 2 |
从而AE2+BE2=4=AB2
∴AE⊥BE.
∵面ADE⊥面ABCE,面ADE∩面ABCE=AE,
∴BE⊥平面ADE,∵AD?平面ADE
∴BE⊥AD
点评:熟练掌握三角形的中位线定理、线面平行的判定定理、勾股定理的逆定理、面面垂直的性质和判定定理、线面垂直的判定定理是解题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
已知集合P={y|y=-x2+2,x∈R},Q={y|y=x,x∈R},则P∩Q=( )
| A、R |
| B、{y|y≤2} |
| C、{y|y≥2} |
| D、{y|y>2} |
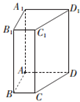 已知四棱柱ABCD-A1B1C1D1,侧棱AA1⊥底面ABCD,底面ABCD中,AB⊥AD,BC∥AD,AB=2,AD=4,侧棱AA1=4.
已知四棱柱ABCD-A1B1C1D1,侧棱AA1⊥底面ABCD,底面ABCD中,AB⊥AD,BC∥AD,AB=2,AD=4,侧棱AA1=4.