题目内容
若双曲线的两条准线之间距离为3,且过点(2,
),求双曲线的标准方程.
| ||
| 3 |
考点:双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:由已知得
=3,从而4a4=9c2=9(a2+b2),由此能求出双曲线的标准方程.
| 2a2 |
| c |
解答:
解:由已知得
=3,
所以4a4=9c2=9(a2+b2),(1)
如果双曲线焦点在x轴上,
则方程为
-
=1,
将x=2,y=
代入得
-
=1,(2)
联立(1)(2),解得a2=3,b2=1,或a2=
,b2=
,
如果双曲线焦点在y轴,则方程为
-
=1,
将x=2,y=
代入得
-
=1,( )
由(1)(3)可得无解.
所以,所求双曲线方程为
-y2=1 或
-
=1.
| 2a2 |
| c |
所以4a4=9c2=9(a2+b2),(1)
如果双曲线焦点在x轴上,
则方程为
| x2 |
| a2 |
| y2 |
| b2 |
将x=2,y=
| ||
| 3 |
| 4 |
| a2 |
| 1 |
| 3b2 |
联立(1)(2),解得a2=3,b2=1,或a2=
| 13 |
| 4 |
| 13 |
| 9 |
如果双曲线焦点在y轴,则方程为
| y2 |
| a2 |
| x2 |
| b2 |
将x=2,y=
| ||
| 3 |
| 1 |
| 3a2 |
| 4 |
| b2 |
由(1)(3)可得无解.
所以,所求双曲线方程为
| x2 |
| 3 |
| x2 | ||
|
| y2 | ||
|
点评:本题考查双曲线方程的求法,是中档题,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
相关题目
设函数f(x),g(x)的定义域分别为F,G,且F?G.若对任意的x∈F,都有g(x)=f(x),则称g(x)为f(x)在G上的一个“延拓函数”.已知函数f(x)=2x(x≤0),若g(x)为f(x)在R上的一个延拓函数,且g(x)是偶函数,则函数g(x)的解析式是( )
| A、2|x| | ||
| B、log2|x| | ||
C、(
| ||
D、log
|
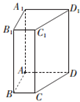 已知四棱柱ABCD-A1B1C1D1,侧棱AA1⊥底面ABCD,底面ABCD中,AB⊥AD,BC∥AD,AB=2,AD=4,侧棱AA1=4.
已知四棱柱ABCD-A1B1C1D1,侧棱AA1⊥底面ABCD,底面ABCD中,AB⊥AD,BC∥AD,AB=2,AD=4,侧棱AA1=4.